Simplification

Review methods to simplify mathematical expressions

Published

August 10, 2024

1 Addition and subtraction of like terms

Like terms are multiples of the same variable raised to the same power, e,g., \(2x\), \(\frac{1}{3}x\), and \(12x\) are like terms.
For example, \(3x\), \(-5x\), and \(7x\) can be simplified as \(3x-5x+7x=5x\).

To remove parentheses, multiply the outside term by each term inside the parentheses.

Simplify \(\displaystyle a (3+4a)\)

\[ a (3+4a)= \]

\[3a+4a^2\]

Simplify \(5b-b(2+7b)\)

\[ 5b-b(2+7b)= \]

\[ 5b-(2b+7b^2) = \]

\[ 5b-2b-7b^2= \]

\[ (5b-2b)-7b^2= \]

\[ 3b-7b^2 \]

Calculate \(\frac{1}{2}(2c-8)\)

The answer is

A binomial is a polynomial expression that has only two terms.
It can be expressed as \(ax^m+bx^n\), where:
- \(x\) is a variable.
- \(a\) and \(b\) are coefficients that can take any real number.
- \(m\) and \(n\) are exponents.

Note 1: Real numbers (\(\mathbb{R}\))

Real numbers include:

Integers (e.g., \(-3, 0, 5\)).
Rational numbers that include ratios of two integers(e.g., \(\frac{1}{4}\)) and decimals that terminate or repeat (e.g., \(3.2\) and \(0.333333333333333\)).
Irrational numbers that cannot be expressed as ratios of two integers (e.g., \(\sqrt{2}\) and \(\pi\)). The decimal of an irrational number does not terminate or repeat. For example, \(\pi\) \(\approx 3.14159265358979323846......\) . Its decimal does not repeat or terminate. Although \(\pi\) is approximated as \(3.14\) or \(22/7\), these are not exact values.

Use the FOIL method (F: multiply firsts, O: multiply outers, I: multiply inners, L: multiply lasts).

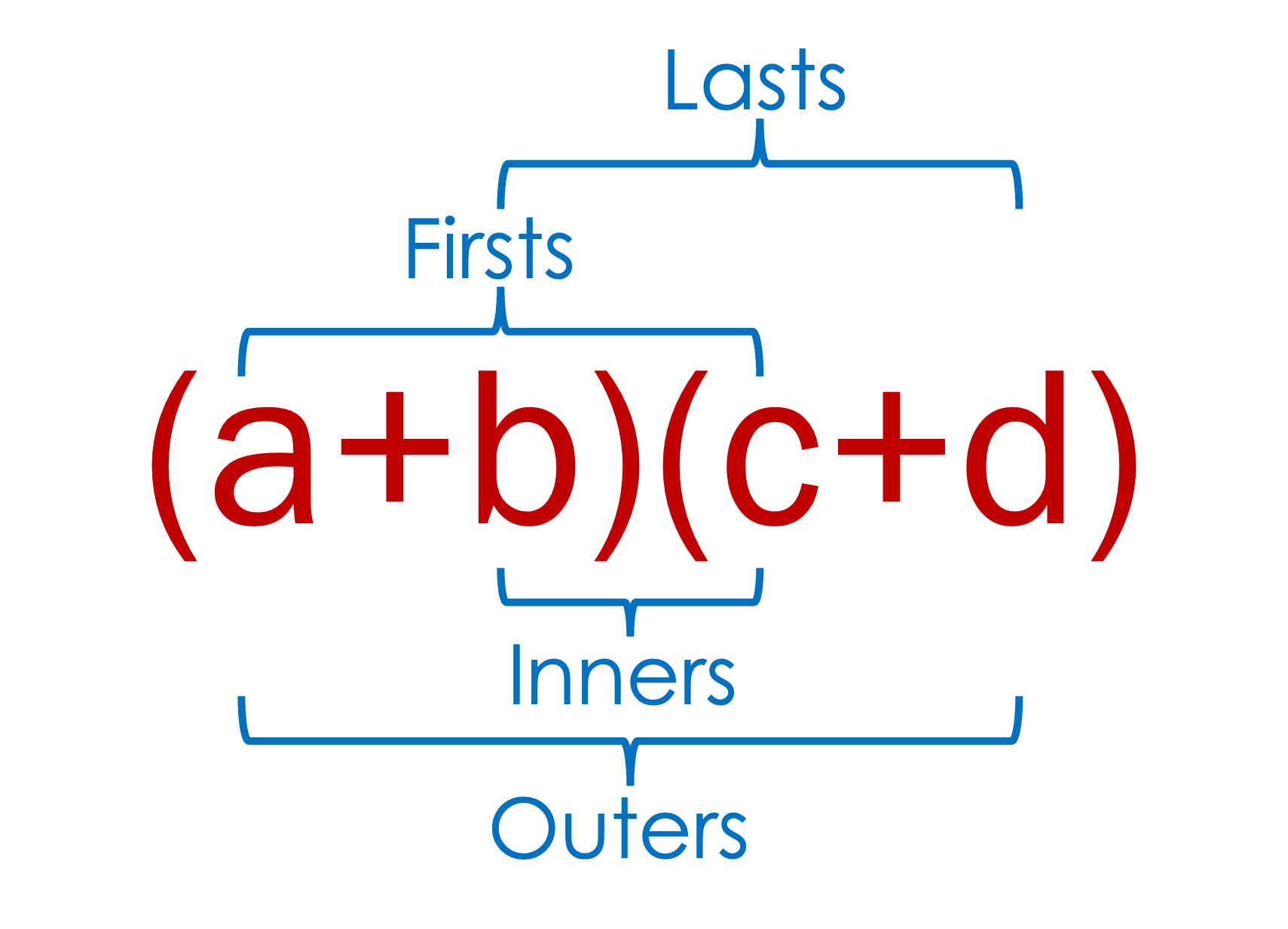
Simplify \((x+5)(x-2)\)

\[ (x+5)(x-2) = \]

\[ x^2-2x+5x-10= \]

\[ x^2+3x-10 \]

Simplify \((y^2-4y)(3-y)\)

\[ (y^2-4y)(3-y)= \]

\[ 3y^2-y^3-12y+4y^2= \]

\[ -y^3+7y^2-12y \]