Exponential and Logarithmic Functions
1 Exponential function
The exponential function has the form \(\displaystyle y= f(x) =a^x\):
\(a\) is a constant known as the base, \(a \gt 0\) and \(a \ne 0\).
\(x\) is the exponent.
The natural exponential function \(y = e^x\) is a specific type of exponential functions where the base is the constant \(e\), known as Euler’s number (\(e \approx 2.718281828459045…\)).
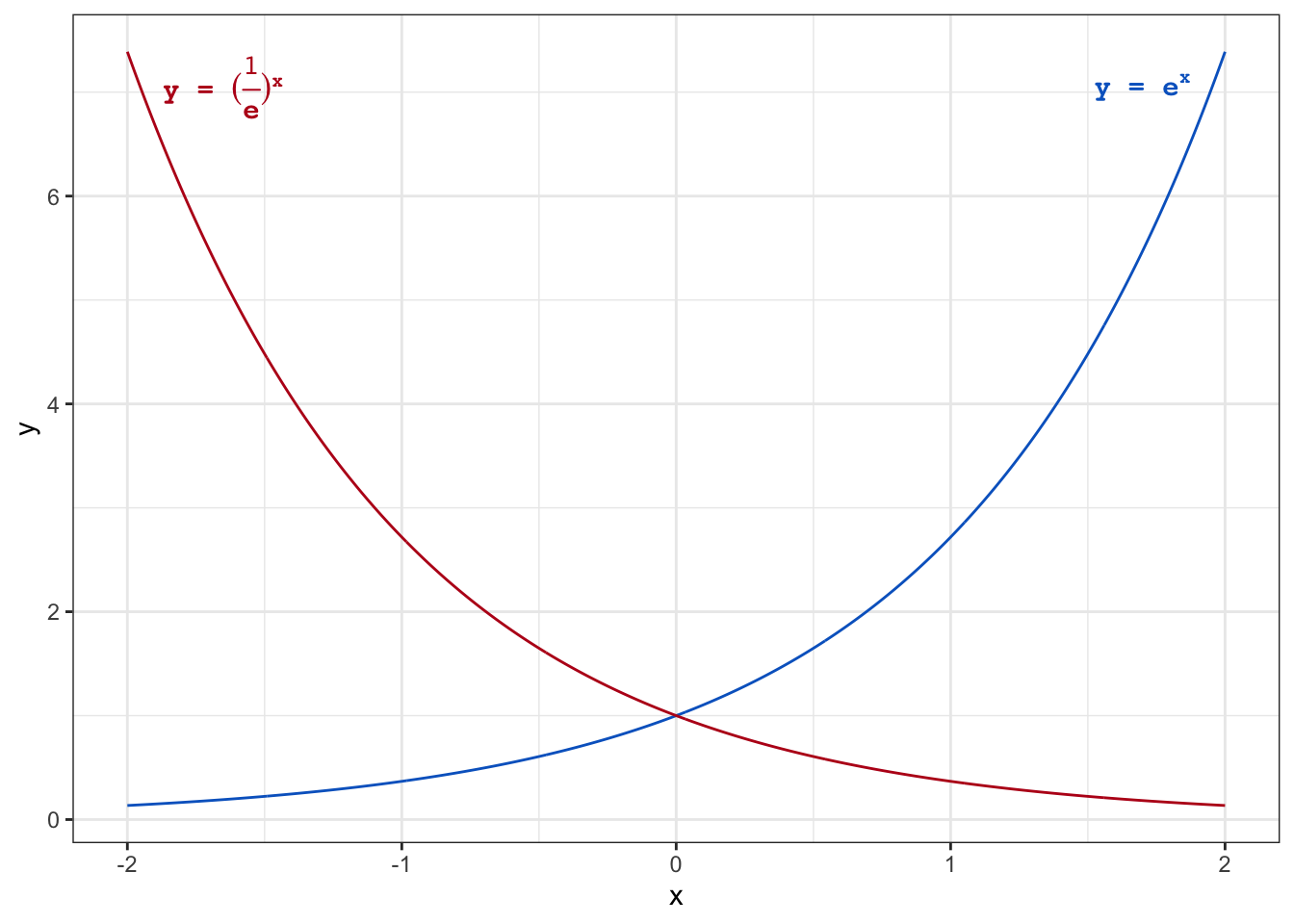
A graphical presentation of an exponential function with bases less or greater than \(1\) is depicted in Figure 1.

2 Logarithmic function
The logarithmic function has the form \(y = f(x) = \log_ax\):
\(a\) is a constant known as the base of logarithm, \(a \gt 0\) and \(a \ne 1\).
\(x \gt 0\) (i.e., the function is defined only if \(x\) is positive).
It is read as \(\log\) to the base \(a\) of \(x\).
If the base \(a=10\), then it is known as the common logarithm (\(\log\)), but if \(a = e\), then it is known as the natural logarithm (\(\ln\)).
R function for the common logarithm is
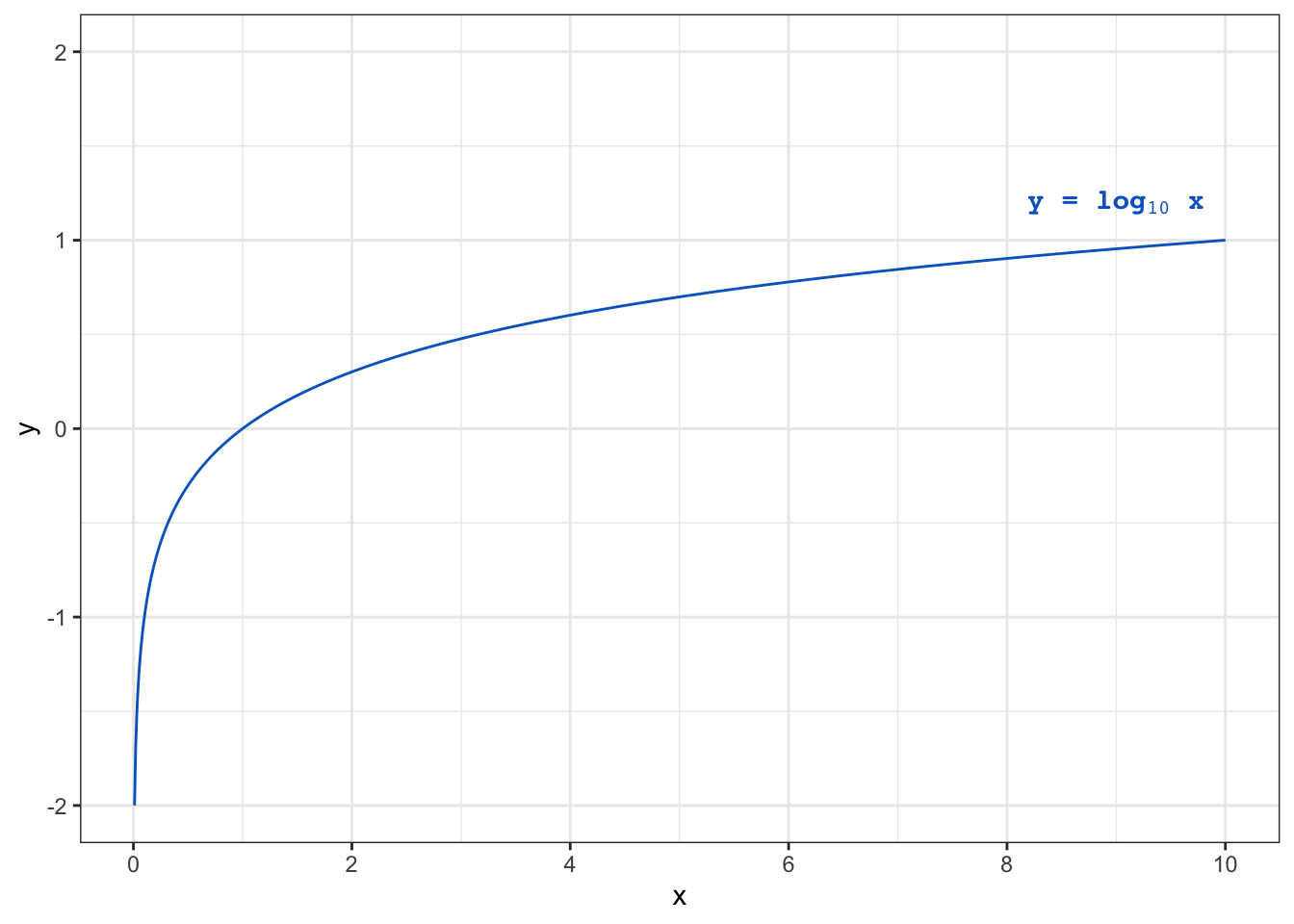
log10()and for the natural logarithm islog().A graphical presentation of the logarithmic function \(y =log_{10}\ x\) is depicted in Figure 2.
3 Relation between exponential and logarithmic functions
Each function is the inverse of the other (i.e., each function undoes the other):
\(a^{\log_ax} = x\), for \(x>0\)
\(\log_a a^x = x\)
If \(a^y = x\), then \(y = \log_a x\).
Similarly, if \(\log_a x = y\), then \(x = a^y\).
4 Basic laws of exponents
\(a^m a^n = a^{m+n}\)
\(\displaystyle \frac{a^m}{a^n} = a^{m-n}\)
\((a^m)^n = a^{mn}\)
\((ab)^n = a^nb^n\)
\(\displaystyle (\frac{a}{b})^n = \frac{a^n}{b^n}\)
\(a^0 = 1\)
\(\displaystyle a^{-n} = \frac{1}{a^n}\)
\(\displaystyle a^{\frac{1}{n}} =\sqrt[n]{a}\), this is referred to as the \(n^{th}\) root of \(a\)
\(\displaystyle a^{\frac{m}{n}} = \sqrt[n]{a^m}\)
Calculate \(\displaystyle \frac{2^7}{2^5} + 4^0\)
\[ \displaystyle \frac{2^7}{2^5} + 4^0 = \] \[ \displaystyle 2^{(7-5)} + 4^0\ {\color{#0466c8}(\text {apply rule 2}\rightarrow)} = \] \[ \displaystyle 2^2 + 1\ {\color{#0466c8}(\text {apply rule 6}\rightarrow)} = \] \[ \displaystyle 4 + 1 = 5 \]
5 Basic laws of logarithms
\(\log_a x^b = b\log_a x\)
\(\log_a (xy) = \log_a x + \log_a y\)
\(\log_a \frac{x}{y} = \log_a x - \log_a y\)
\(\log_a x = \displaystyle \frac{\log_b x}{\log_b a}\)
\(\log_a x = \displaystyle \frac{1}{\log_x a}\)
\(\log_a 1 = 0\)
\(\log_a a = 1\)
Write \((4 \log_{10} x + 3 \log_{10} 5y)\) as a single logarithm.
\[ 4 \log_{10} x + 3 \log_{10} 5y = \]
\[ \log_{10} x^4 + \log_{10} (5y)^3 {\color{#0466c8}(\text {apply rule 1}\rightarrow)} = \] \[ \log_{10} x^4 \cdot (5y)^3 {\color{#0466c8}(\text {apply rule 2}\rightarrow)} = \] \[ \log_{10} 125 x^4 y^3 \]
To apply the above manipulations, the base of the logarithm should be the same for all terms.
Solve the equation \(125^{x-2} = 5^{2-x}\) for \(x\)
\[ 125^{x-2} = 5^{2-x} \Rightarrow \] \[ (5^3)^{x-2} = 5^{2-x} \Rightarrow \] \[ 5^{3 (x-2)} = 5^{2-x} \Rightarrow \] \[ 5^{3x-6} = 5^{2-x} \Rightarrow \] \[ 3x-6 = 2-x \Rightarrow \] \[ 3x+x = 2+6 \Rightarrow \] \[ 4x = 8 \Rightarrow \] \[ x = 2 \]
Solve the equation \(\log_2 (3y-1) = 3\) for \(y\)
The answer is \(y =\)
If \(y = \log_a x\), then \(a^y = x\)
Solve the equation \(3\ln (\sqrt[3]{y-e}) - \ln 2 = 1\) for \(y\)
The answer is \(y =\)
6 References
Exponential and Logarithmic Functions. Byju’s. Retrieved August 24, 2024, from https://byjus.com/maths/exponential-and-logarithmic-functions/
Chapman, A., G., Herald, M., & Libertini, J. Logarithms and Exponential Functions. In APEX PreCalculus. LibreTexts. Retrieved August 24, 2024, from https://math.libretexts.org/Bookshelves/Precalculus/APEX_PreCalculus_(Chapman_Herald_and_Libertini)/01%3A_Numbers_and_Functions/1.05%3A_Logarithms_and_Exponential_Functions