Integration

Review basic laws of integration
Published

September 5, 2024


1 The idea of integration

  • Integration is considered the reverse process of differentiation.

  • So, it is used to find the original function \(f(x)\) from its derivative \(f'(x)\).

  • Let \(\displaystyle y = x^3+ 2x\), the first derivative is \(\displaystyle \frac{dy}{dx} = 3x^2 + 2\). Inversely, we say that the integral of \(\displaystyle 3x^2 + 2\) with respect to \(x\) is \(\displaystyle x^3 + 2x + c\), where \(c\) is the constant of integration.

  • Adding this constant is important because the derivative \(\displaystyle \frac{dy}{dx} = 3x^2 + 2\) could have been obtained from different functions, e.g., \(\displaystyle x^3 + 2x + 1\) or \(\displaystyle x^3 + 2x - 25\), etc.

  • During the integration process, the constant term in the original function is unknown, therefore, the constant of integration \(c\) is added to account for this unknown term.

  • The integration of the above function is denoted by \(\displaystyle \int (3x^2 + 2)dx = x^3 + 2x + c\):

    • The symbol \(\displaystyle \int\) is the integral sign.

    • The function to be integrated is known as the integrand.

    • The term \(dx\) indicates the variable with respect to which the integration is carried out.

    • \(c\) is the constant of integration.

  • Types of integrals:

    • Indefinite integral:

      • The integral of a function without limits, e.g., \(\displaystyle \int f(x)dx\).

      • The result is a function with an unknown constant of integration.

    • Definite integral:

      • The integral of a function over a specific interval, e.g., \(\displaystyle \int_{a}^{b} f(x)dx\).

      • The result is a number.

      • \(a\) and \(b\) are numbers known as the lower and upper limits of the integral, respectively.

2 Basic rules of integration

  • The following table summarizes the integrals of basic functions:
Table of integrals of basic functions
Function \(f(x)\) Integral \(\displaystyle \int f(x)dx\)
Constant \(k\) \(kx + c\)
\(x\) \(\displaystyle \frac{1}{2}x^2 + c\)
\(x^n\) \(\displaystyle \frac{1}{n+1}x^{n+1}\), where \(n \ne -1\)
\(kx^n\) \(\displaystyle \frac{k}{n+1}x^{n+1}\), where \(n \ne -1\)
\(\displaystyle \frac{1}{x} = x^{-1}\) \(\displaystyle \ln |x| + c\)
\(e^x\) \(e^x + c\)
\(e^{kx}\) \(\displaystyle \frac{1}{k}e^{kx} + c\)
\(e^{-x}\) \(-e^{-x} + c\)

  • Rules of integration:

    • \(\displaystyle \int k f(x)dx = k \int f(x)dx\), where \(k\) is a constant.

    • \(\displaystyle \int \Big( f(x) \pm g(x) \Big)dx = \int f(x)dx \pm \int g(x)dx\).

Find \(\displaystyle \int (2x^3 + \frac{2}{x}- \sqrt{x})\ dx\)

\[ \displaystyle \int (2x^3 + \frac{2}{x}- \sqrt{x})\ dx = \displaystyle 2\int x^3dx + \displaystyle 2\int \frac{1}{x}dx - \displaystyle \int x^{\frac{1}{2}}dx = \] \[ 2(\frac{1}{4}x^4 + c_1) + 2(\ln |x| + c_2) - (\frac{2}{3}x^{\frac{3}{2}} + c_3) = \] \[ \frac{1}{2}x^4 + 2\ln |x| - \frac{2}{3}x^{\frac{3}{2}} + C,\ \text{where}\ C = c_1 + c_2 + c_3 \]

Find \(\displaystyle \int (3x^2 + 2x - e^x)\ dx\)

\[ \displaystyle \int (3x^2 + 2x - e^x)\ dx = \displaystyle 3\int x^2dx + \displaystyle 2\int xdx - \displaystyle \int e^xdx = \]

\[ 3(\frac{1}{3}x^3 + c_1) + 2(\frac{1}{2}x^2 + c_2) - (e^x + c_3) = \]

\[ x^3 + x^2 - e^x +C \]

3 Definite integrals

  • The definite integral of a function \(f(x)\) over an interval \([a, b]\) is denoted by \(\displaystyle \int_{a}^{b} f(x)dx\) and is read as “the integral of \(f(x)\) from \(a\) to \(b\)”.

  • \(\displaystyle \int_{a}^{b} f(x)dx = F(b) - F(a)\), where \(F(x)\) is the integral of \(f(x)\).

  • The definite integral of a function is a number, not a function, and does not contain the constant of integration.

  • Example: Find \(\displaystyle \int_{2}^{5} 4x^3dx\)

    • \(\displaystyle \int 4x^3dx = \frac{\cancel{4}}{\cancel{4}}x^4 + c = x^4 + c\).

    • So, \(F(x) = x^4\).

    • \(\displaystyle \int_{2}^{5} 4x^3dx = F(5) - F(2) = 5^4 - 2^4 = 625 - 16 = 609\).

    • There is a shorthand notation for the difference between the two values of \(F(x)\): \(\displaystyle F(b) - F(a) = \Big[ F(x) \Big]_{a}^{b}\)

      Note

      \(\displaystyle \int_{a}^{b} f(x)dx = - \displaystyle \int_{b}^{a} f(x)dx\)

    • The above example can be written as \(\displaystyle \int_{2}^{5} 4x^3dx = \Big[ x^4 \Big]_{2}^{5} = 5^4 - 2^4 = 609\).

Find the definite integral \(\displaystyle \int_{1}^{4} (2x^2 + 5x - 3)\ dx\)

\[ \displaystyle \int_{1}^{4} (2x^2 + 5x - 3)\ dx = \Bigg[ \frac{2}{3}x^3 + \frac{5}{2}x^2 - 3x \Bigg]_{1}^{4} = \] \[ \left( \frac{2}{3} \times 4^3 + \frac{5}{2} \times 4^2 - 3 \times 4 \right) - \left( \frac{2}{3} \times 1^3 + \frac{5}{2} \times 1^2 - 3 \times 1 \right) = \frac{141}{2} = 70.5 \]

Find the definite integral \(\displaystyle \int_{2}^{4} e^{2x} dx\)

\[ \displaystyle \int_{2}^{4} e^{2x} dx = \Bigg[ \frac{1}{2}e^{2x} \Bigg]_{2}^{4} = \frac{1}{2} \Bigg[ e^{2x} \Bigg]_{2}^{4} = \frac{1}{2} \left( e^8 - e^4 \right) \approx 1463.18 \]

3.1 The use of definite integrals to calculate the area under a curve

  • The area under a curve (AUC) is an essential concept in calculus and statistics.

  • It can be calculated using definite integrals.

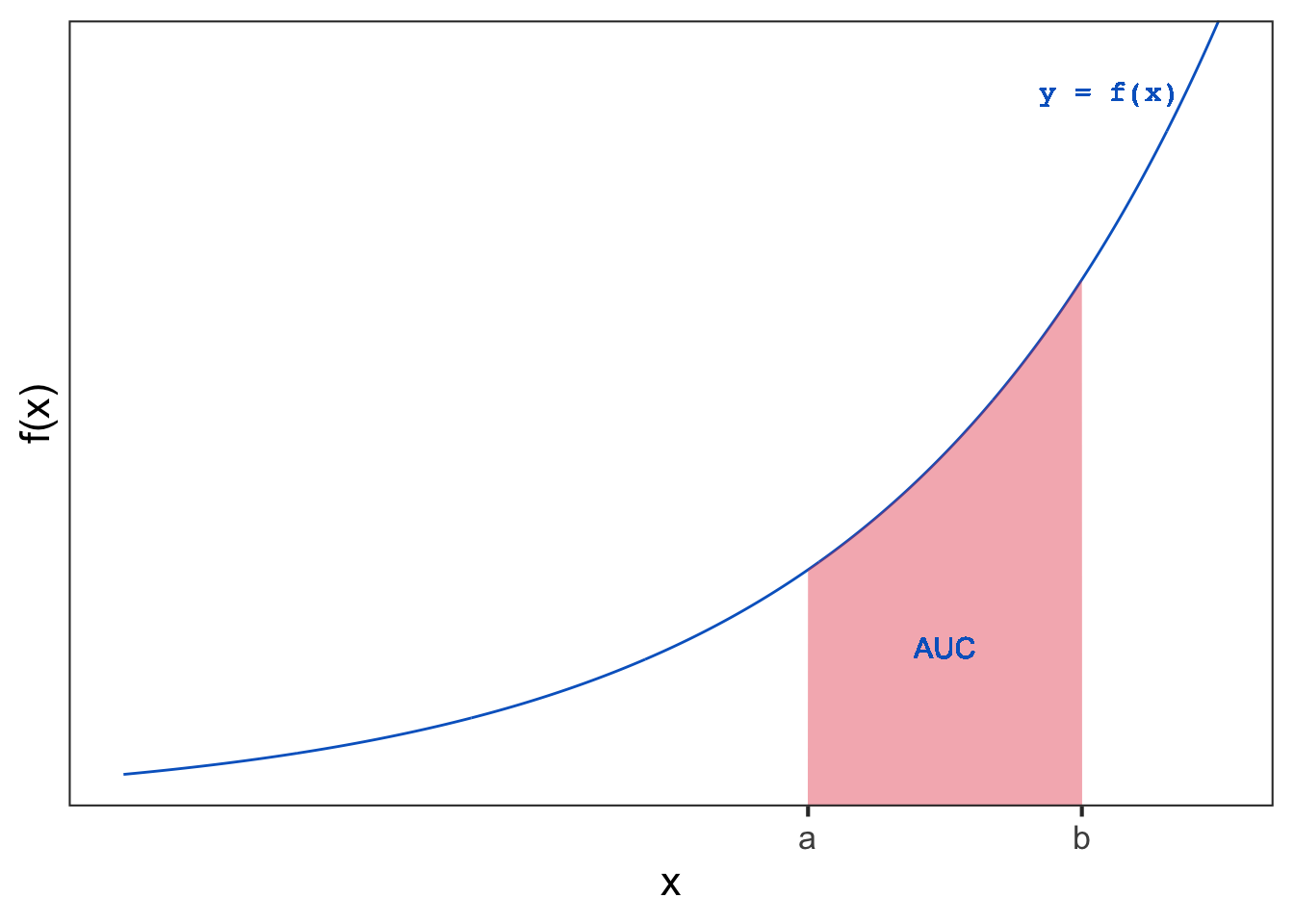
  • For example, let \(y = f(x)\) be a continuous function of \(x\) and represented by the following graph:

  • The shaded area represents the area under the curve above the \(x\)-axis and between the points \(x = a\) and \(x = b\).

  • This area can be calculated by finding the definite integral of the function \(f(x)\) over the interval \([a, b]\).

  • AUC = \(\displaystyle \int_{a}^{b} f(x)dx\).

  • Example: Calculate the area under the curve \(\displaystyle y = e^{-0.4x}\) above the \(x-\)axis and between \(x = -3\) and \(x = 2\):

    • The curve is represented by following graph:

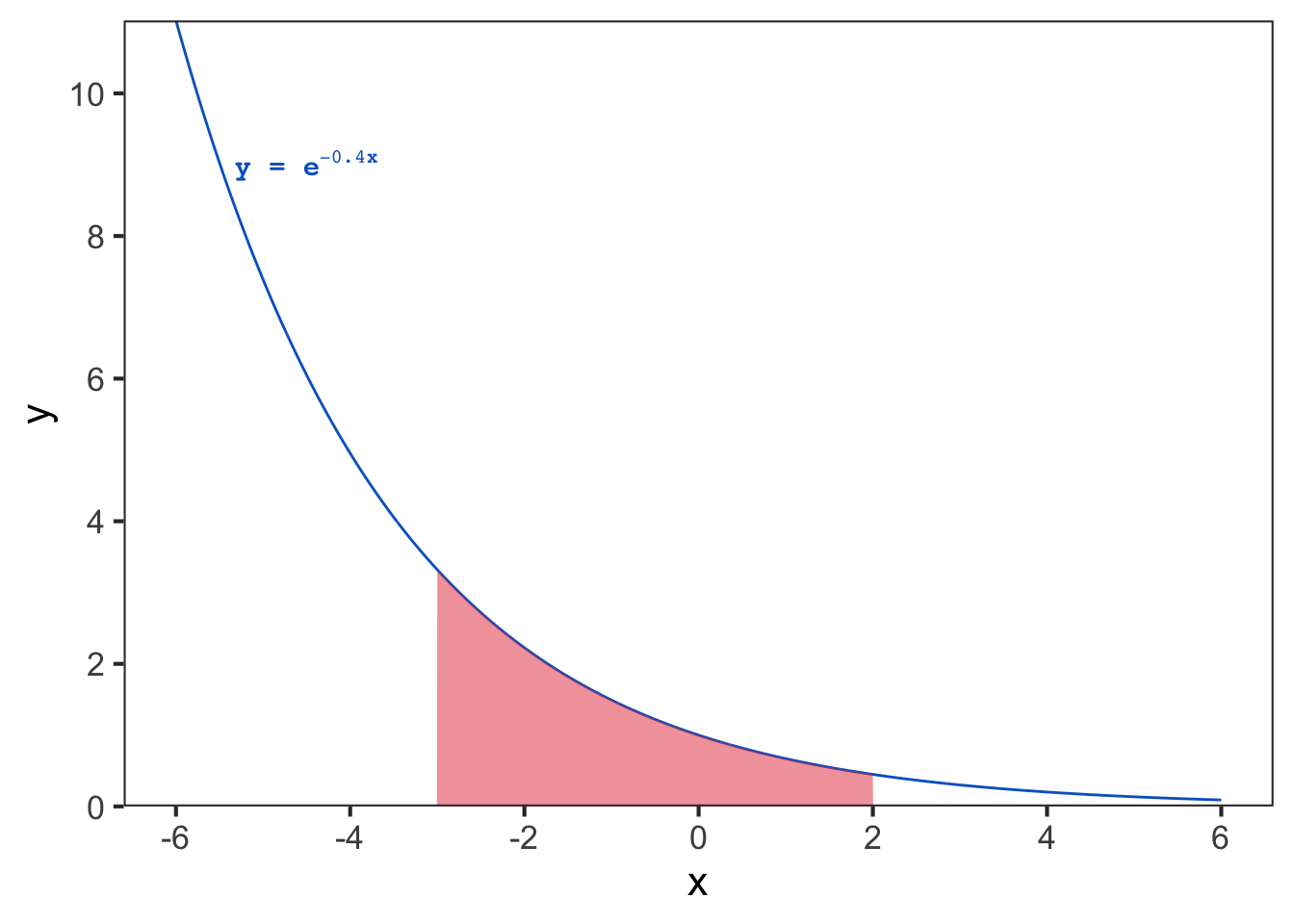
    • The area under the curve above the \(x-\)axis and between \(x = -3\) and \(x = 2\) is \(\displaystyle \int_{-3}^{2} e^{-0.4x}dx = \Big[ -\frac{5}{2}e^{-0.4x} \Big]_{-3}^{2} = -\frac{5}{2}e^{-0.8} - \Big(-\frac{5}{2}e^{1.2} \Big) \approx 7.177\).

4 Integration by substitution

  • This technique is used to simplify the integration of complex functions.

  • It involves substituting a new variable, say \(u\), for a more complicated part of the function to be integrated (i.e., the integrand).

  • The method of choosing the best substitution needs practice and experience.

  • Example: Find \(\displaystyle \int (2x + 1)^3dx\):

    • Let \(u = 2x + 1\) (i.e., substitute \(u\) for the more complex part of the integrand).

    • Differentiate \(u\) with respect to \(x\) to find \(dx\) in terms of \(du\), \(\displaystyle \frac{du}{dx} = 2 \Rightarrow {\color{#0466c8} {dx = \frac{du}{2}}}\).

    • Now, the original integral \(\displaystyle \int (2x + 1)^3dx\) becomes \(\displaystyle \int u^3 dx =\displaystyle \int u^3 \frac{du}{2} = \frac{1}{2} \cdot \frac{1}{4}u^4 +c = \frac{1}{8}u^4 +c\).

      Note

      In this step, the new integral with respect to \(u\) should not contain any terms involving \(x\).

    • Substitute back \(u = 2x + 1\) to get \(\displaystyle \frac{(2x + 1)^4}{8} + c\).

4.1 Definite integrals by substitution

  • The above described method can also be used to evaluate definite integrals.

  • Example: Find \(\displaystyle \int_{1}^{3} (2x + 1)^3dx\), apply the above mentioned steps:

    • Let \(u = 2x +1 \Rightarrow dx =\displaystyle \frac{du}{2}\).

    • In this step, we have to find the integral limits in terms of \(u \Rightarrow\) when \(x = 1, u = 2 \times 1 + 1 = 3\) and when \(x = 3, u = 2 \times 3 + 1 = 7\).

    • The original integral \(\displaystyle \int_{1}^{3} (2x + 1)^3dx\) becomes \(\displaystyle \int_{3}^{7} u^3 \frac{du}{2} = \frac{1}{8} \Big[ u^4 \Big]_{3}^{7} = \frac{1}{8} \left( 7^4 - 3^4 \right) = 290\).

Find \(\displaystyle \int \frac{8x^3-3}{2x^4-3x+1}\ dx\)

  • Let \(\displaystyle u = 2x^4 - 3x + 1 \Rightarrow \frac{du}{dx} = 8x^3 - 3 \Rightarrow du = (8x^3 - 3)\ dx\).

  • The integral \(\displaystyle \int \frac{8x^3-3}{2x^4-3x+1}\ dx\) becomes \(\displaystyle \int \frac{1}{u}\ du = \ln |u| + c = \ln |2x^4 - 3x + 1| + c\).

    Note

    From the above example, The following rule can be derived: \[ \displaystyle \int \frac{f'(x)}{f(x)}dx = \ln |f(x)| + c \]

5 Integration by parts

  • This technique is used to integrate the product of two functions.

  • Let \(f(x)\) and \(g(x)\) be two functions, then \(\displaystyle \int f(x)g(x)dx = f \int g(x)dx - \int \Big( f'(x) \int g(x)dx \Big)\ dx\).

  • This can be expressed in another way given the functions \(u\) and \(v\), \(\displaystyle \int u v'\ dx = uv - \int u'v\ dx\), where \(u = f(x)\) and \(v' = g(x)\).

  • For definite integrals by parts, \(\displaystyle \int_{a}^{b} u v'\ dx = \Big[ uv \Big]_{a}^{b} - \int_{a}^{b} u'v\ dx\).

  • Example: Find \(\displaystyle \int x e^x dx\):

    • Let \(u = x \Rightarrow u' = 1\) and \(\displaystyle v' = e^x \Rightarrow v = \int e^xdx = e^x\).

    • Using the above rule \(\displaystyle \int u v'\ dx = uv - \int u'v\ dx \Rightarrow \int x e^x\ dx = xe^x - \int 1 \cdot e^x\ dx\).

      Note

      • In this step, there is no need to add the integration constant \(c\).

      • It can be added at the final step.

    • Therefore, the integral \(\displaystyle \int x e^x dx = xe^x - e^x + c\).

Find \(\displaystyle \int_{3}^{6} 4x^3 \ln x\ dx\)

The answer rounded to two decimal places is

6 References


7 Add your comments

Back to top