Basic Concepts

Published

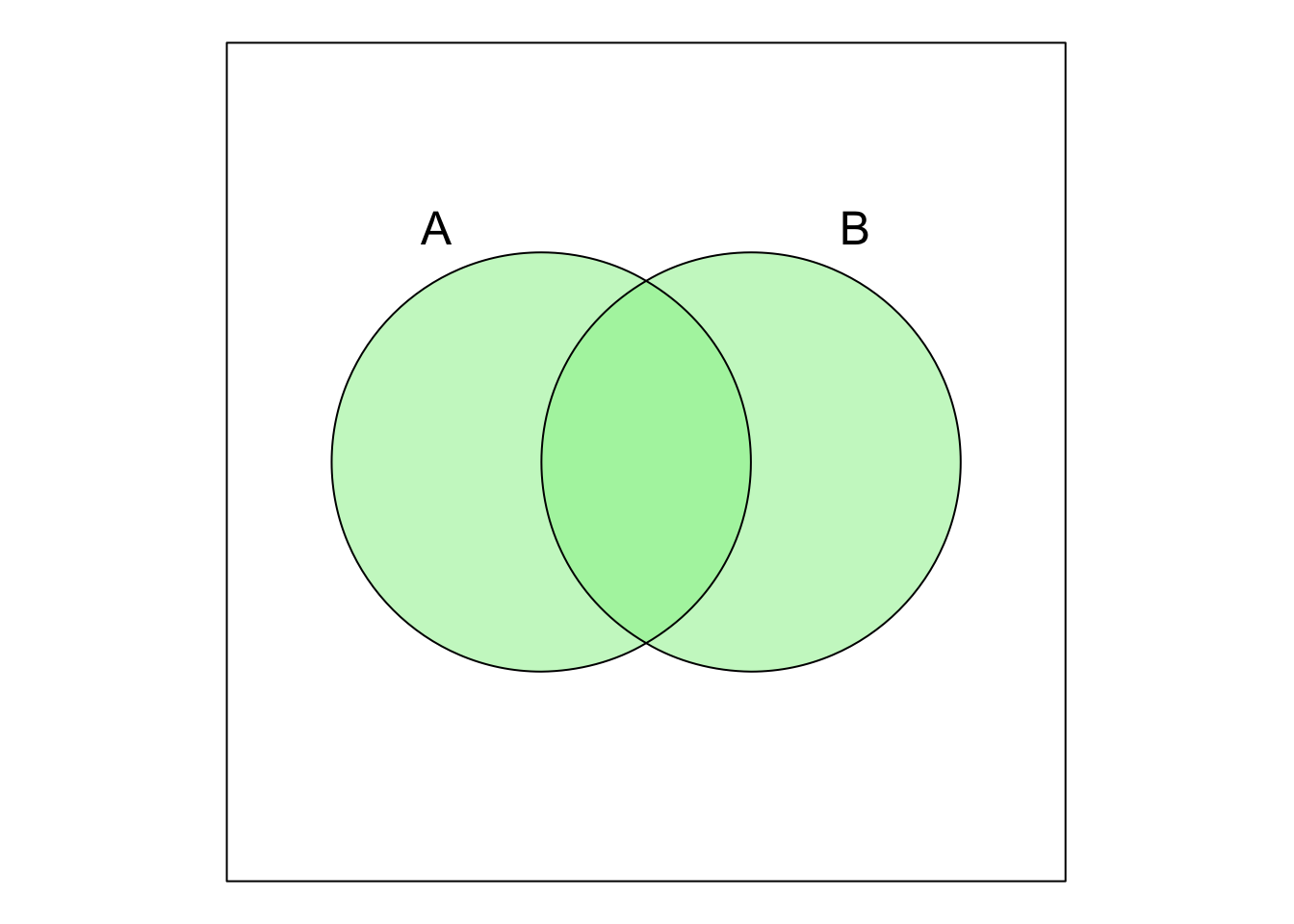
December 2, 2024

1 Sample Space

When we perform a random experiment, the set of all possible outcomes is called the sample space and is denoted by \(S\) or \(\Omega\).

Note

A random experiment is an experiment that can be repeated many times under the same conditions and its outcome is uncertain (can be known only after the experiment is performed).

Example 1:
- Let’s assume that we are interested in answering the question “Are customers satisfied with the quality of a product?”:
  - We can select a random sample of customers and ask them about their satisfaction (satisfied or not satisfied).
  - The sample space: \(S = \{\text{satisfied, not satisfied}\}\)
Example 2:
- Let’s assume that we are interested in answering the question “How many days you go shopping per week?”:
  - We can select a random sample of people and ask them about the number of days they go shopping per week.
  - The sample space: \(S = \{0, 1, 2, 3, 4, 5, 6, 7\}\)
The sample space can be finite, countably infinite, or infinite.
Note
- A countably infinite set contains infinite elements, however, its elements can be put in one-to-one correspondence with the set of natural numbers \(\mathbb{N}\) (positive integers: \({1, 2, 3, \ldots}\))
- This simply means the elements can be listed sequentially using the natural numbers without skipping any element.
- For example the set of integers \(\mathbb{Z} = \{\ldots, -3, -2, -1, 0, 1, 2, 3, \ldots\}\) is a countably infinite set:
  - It has infinite elements that can be listed sequentially using the natural numbers: \(1 \rightarrow 0, 2 \rightarrow 1, 3 \rightarrow -1, 4 \rightarrow 2, 5 \rightarrow -2, 6 \rightarrow 3, \ldots\).

An event is a subset of the sample space \(S\) and is denoted by uppercase letters \(A, B, C, \ldots\).
For an event \(A\) that belongs to the sample space \(S\), we write \(A \subseteq S\).
\(S\) is considered an event as it contains all the possible outcomes (because \(S\) will always occur it is referred to as a certain or sure event).
The empty or null set \(\emptyset = \{\}\) is also considered an event (this event will never occur and is referred to as an impossible event).
The event that contains a single possible outcome of the random experiment is referred to as a simple event or an elementary event.
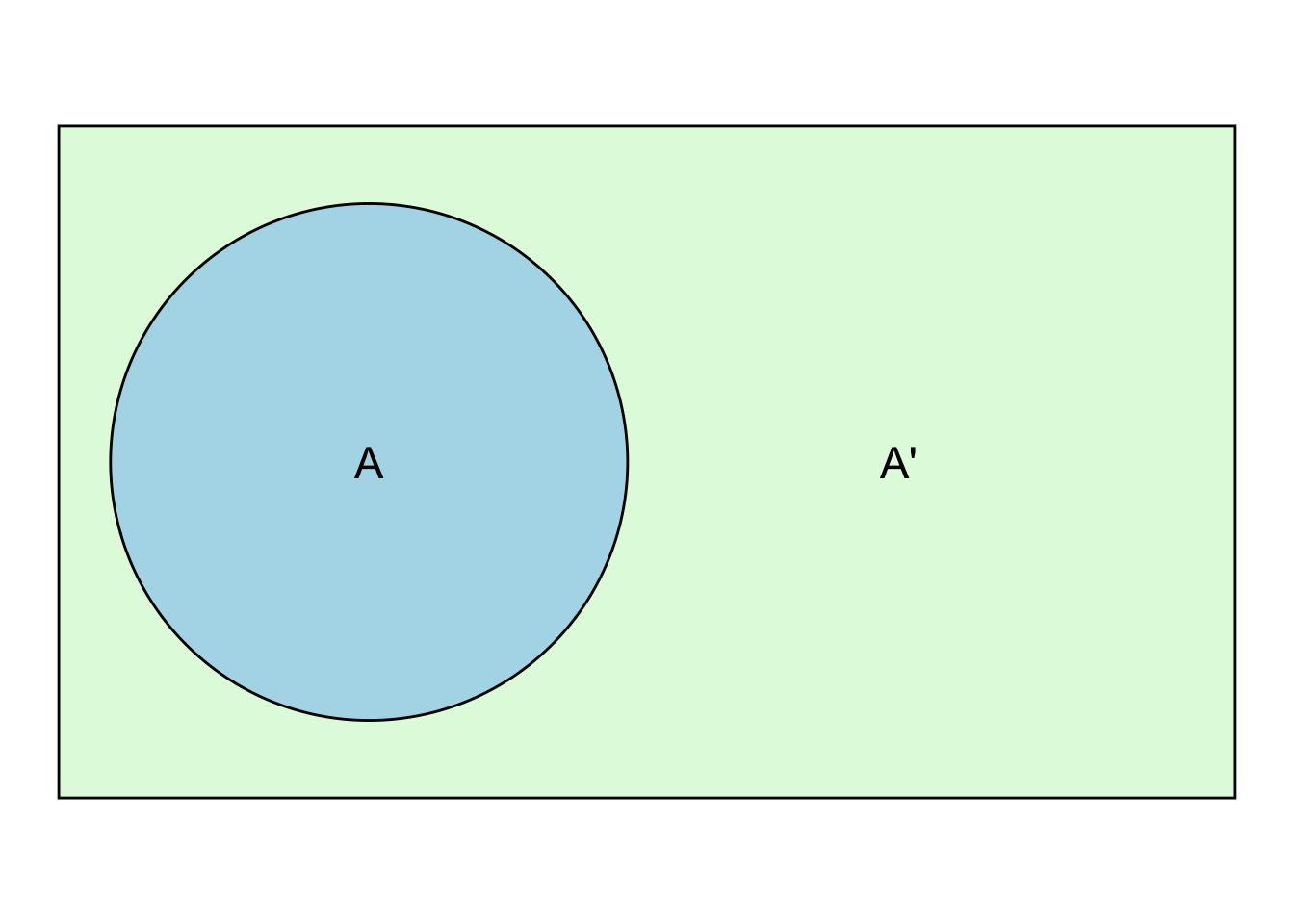
\(A^c = A' = \bar{A}\) is known as the complement of \(A\) and contains the elements that are in \(S\) but not in \(A\).

Assume a dice is rolled and we are interested in the number that appears on the top face:

Example C.1.1

The sample space (sure event): \(S = \{1, 2, 3, 4, 5, 6\}\).
The event of getting a particular number (e.g., \(3\)) is an elementary event: \(A = \{3\}\) (\(A \subset S\)).
The event of getting an even number: \(B = \{2, 4, 6\}\) (\(B \subset S\)).
The event of getting an odd number: \(C = \{1, 3, 5\}\) (\(C \subset S\)).
The event of getting a number divisible by \(3\): \(D = \{3, 6\}\) (\(D \subset S\)).
The event of getting a negative number: \(E = \emptyset\) (\(E \subset S\)), is an impossible event.

\(A \cup B\) is known as the union of \(A\) and \(B\) and contains the elements that are in \(A\) or \(B\) or both (green-shaded).
Click to show/hide code
```
library(venn)

venn(2, zcolor = "lightgreen", opacity = 0.5, sncs = 1.5)
```
\(A \cap B\) is known as the intersection of \(A\) and \(B\) and contains the elements that are in both \(A\) and \(B\) (blue-shaded).
Click to show/hide code
```
library(venn)
venn("1-, 11, -1", zcolor = "white, dodgerblue, white", sncs = 1.5)
```
If \(A \cap B = \emptyset\), then \(A\) and \(B\) are said to be mutually exclusive or disjoint events.
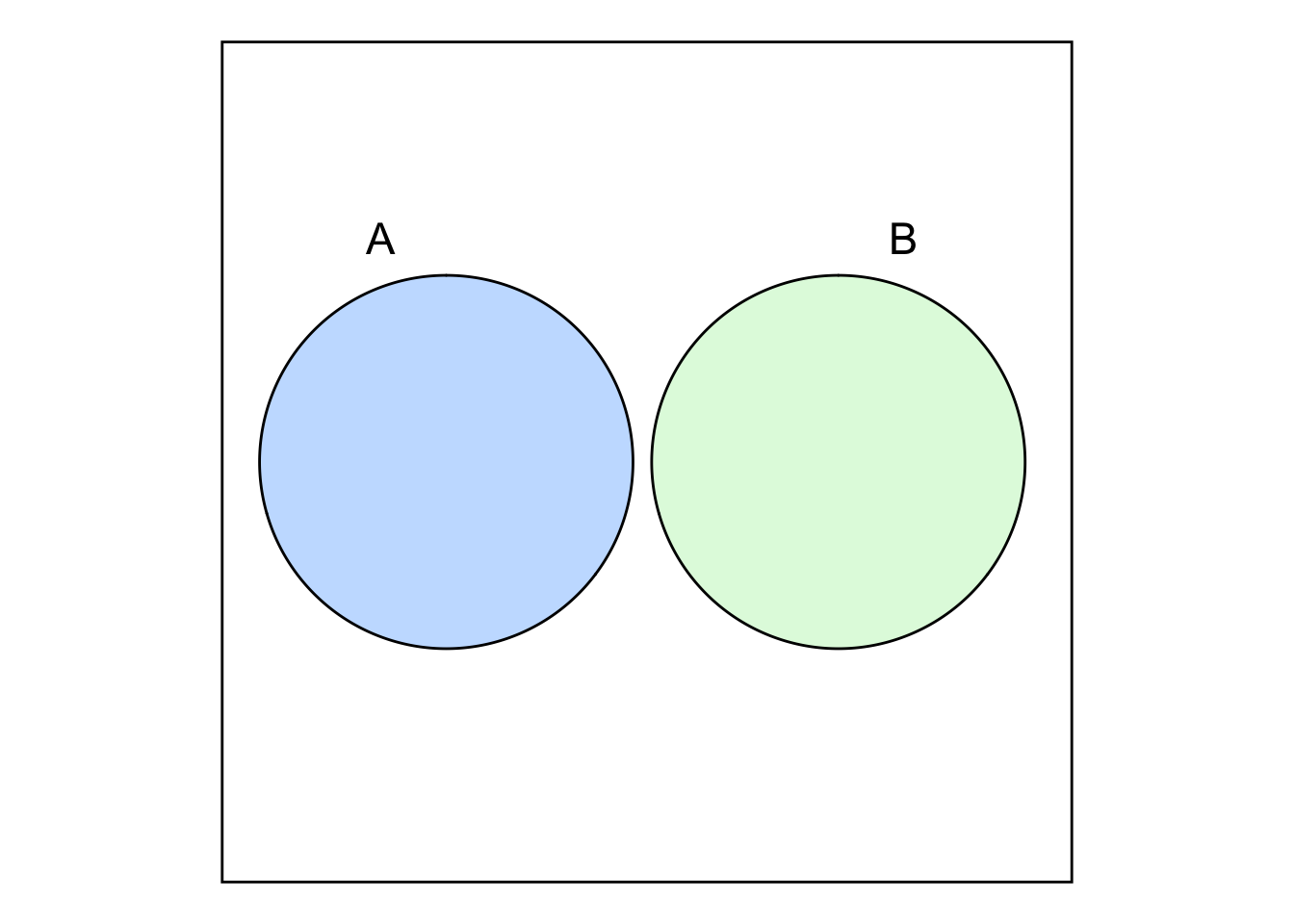
The events \(A_1, A_2, \ldots, A_n\) are mutually or pairwise disjoint, if \(A_i \cap A_j = \emptyset\) for \(i \ne j = 1, 2, \ldots, n\).
If the events \(A_1, A_2, \ldots, A_n\) are pairwise disjoint and \(A_1 \cup A_2 \ldots \cup A_n = S\), then the events are said to be mutually exclusive (i.e., no element belongs to more than one event) and exhaustive (the events together cover the entire sample space) events.
\(A'\) (complement of \(A\)) contains the elements that are in \(S\) (green-shaded) but not in \(A\) (blue-shaded). It is also described as the difference between \(S\) and \(A\), which is denoted by \(S \setminus A\).
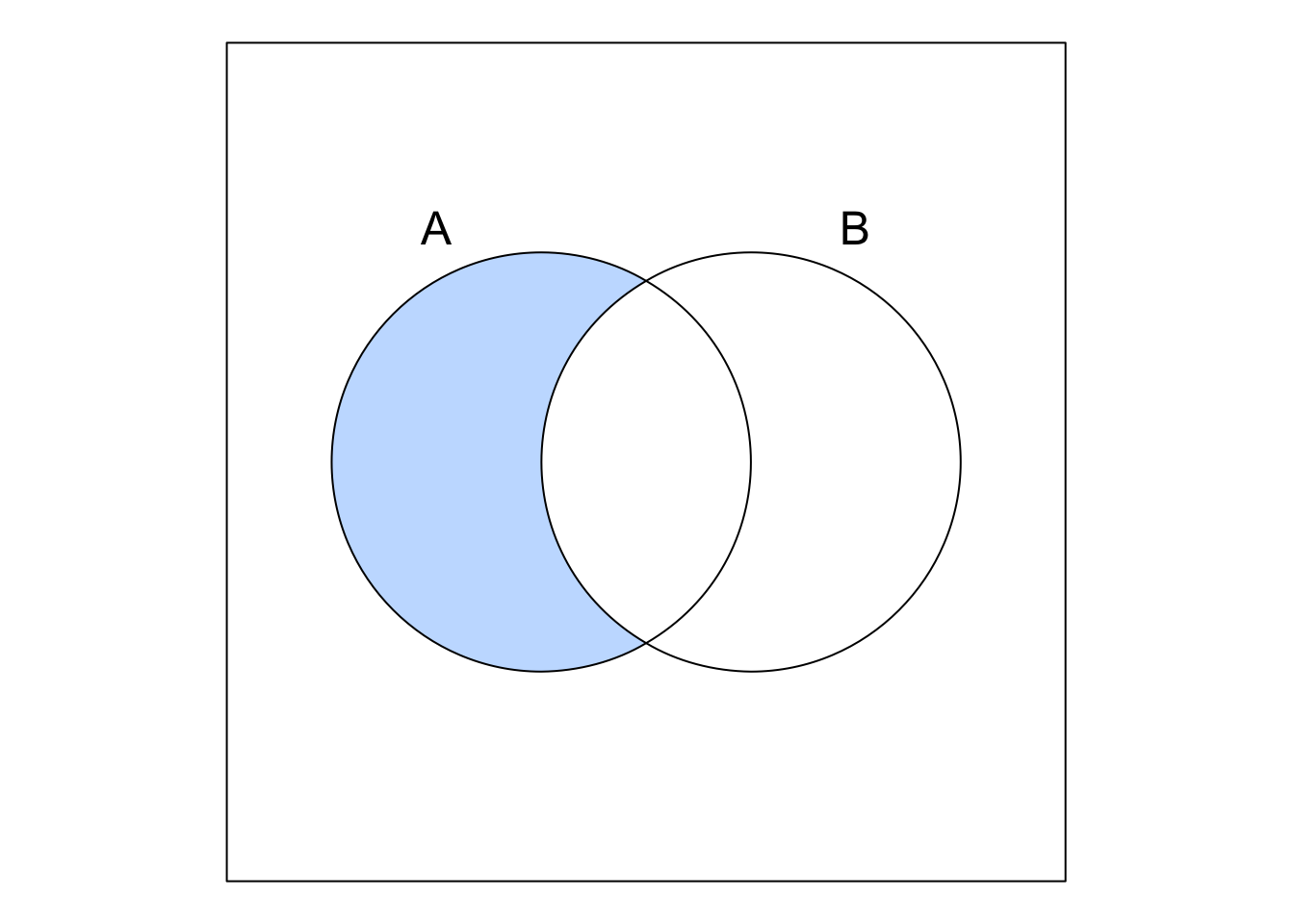
\(A \setminus B = A - B\) is known as the difference between \(A\) and \(B\) and contains the elements that are in \(A\) but not in \(B\) (blue-shaded area).

Note

The figures used above to visualize the set operations are called Venn diagrams.
Each set is represented by a circle, and the overlap between the circles represents the intersection between the sets.

In Example C.1.1, we defined different events based on the outcomes of rolling a dice.
Let’s define some new events to apply the set operations:
- The event of getting an even number or divisible by \(3\) is the union of the events \(B = \{2,4,6\}\) and \(D = \{3,6\}\): \(B \cup D = \{2,3,4,6\}\).
- The event of getting an even number and divisible by \(3\) is the intersection of the events \(B = \{2,4,6\}\) and \(D = \{3,6\}\): \(B \cap D = \{6\}\).
- The event of getting an even number not divisible by \(3\) is the difference between the events \(B = \{2,4,6\}\) and \(D = \{3,6\}\): \(B \setminus D = \{2,4\}\).
- The event of getting an odd number is the complement of the event of getting an even number \(B = \{2,4,6\}\): \(B' = \{1,3,5\}\).

Heumann, C., Schomaker, M., and Shalabh (2022). Introduction to Statistics and Data Analysis: With Exercises, Solutions and Applications in R. Springer
Daniel, W. W. and Cross, C. L. (2013). Biostatistics: A Foundation for Analysis in the Health Sciences, Tenth edition. Wiley
Penn State University. STAT 414: Introduction to Probability Theory. Online Statistics Education. Retrieved December 02, 2024, from https://online.stat.psu.edu/stat414