Measures of Variability

1 Background

• Variability describes how the observations are dispersed around the center of the data.

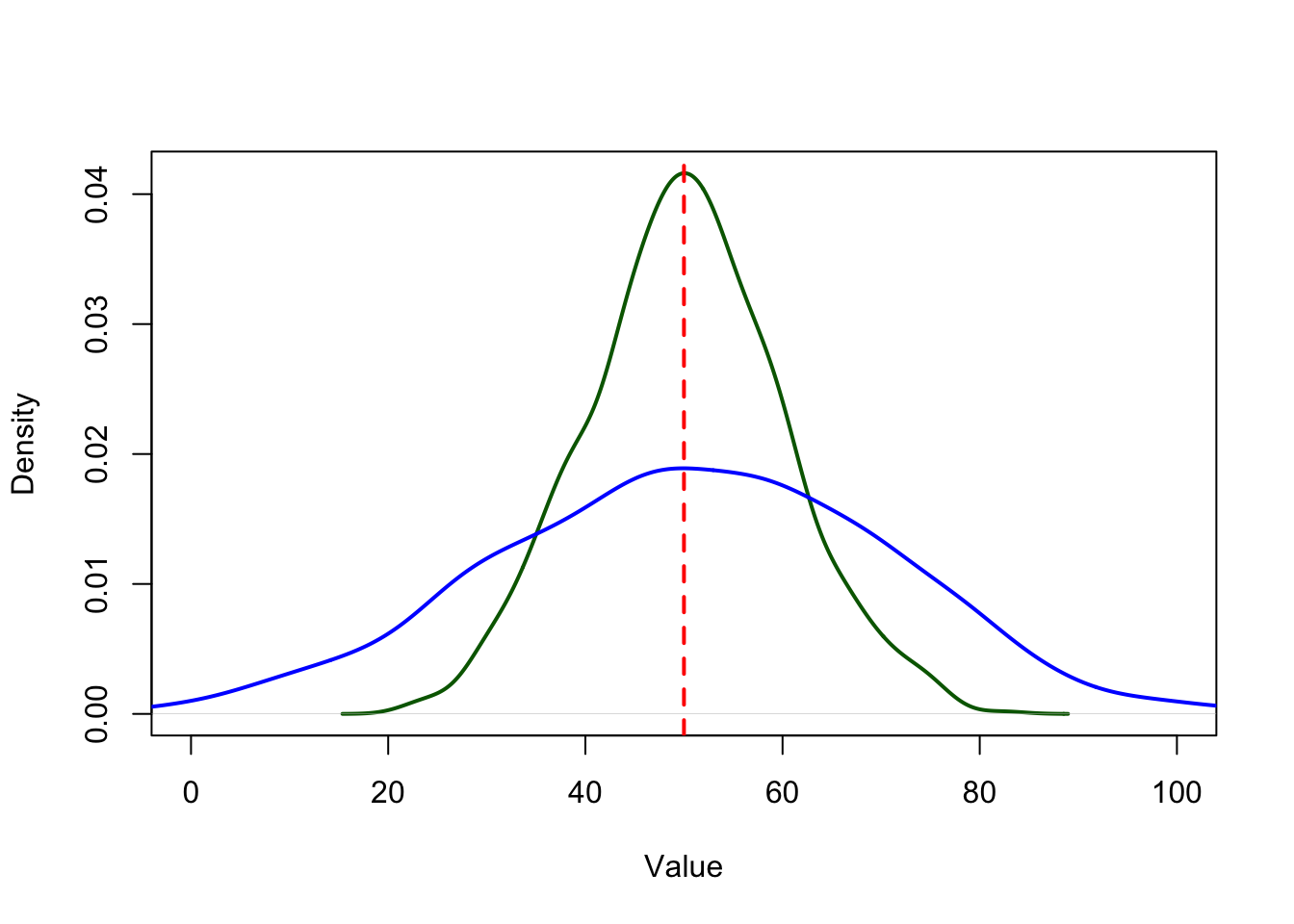
• The terms variability and dispersion are used interchangeably.

• Two distributions can have the same mean but different variability (as depicted in the figure below).

  

  • Despite having the same mean represented by the red vertical line, the blue distribution has a higher variability than the green distribution (i.e., the observations are more dispersed around the mean).

• Therefore, it is important to report a measure of variability along with the measure of central tendency to provide a complete description of the data.

2 Measures of variability

• In the following sections, we will discuss the most commonly used measures of variability.

2.1 Range

• The range \((R)\) is defined as the difference between the maximum and minimum value of the data.

\[ R = x_{\text{max}} - x_{\text{min}} \]

• The range considers only two observations, so its use is limited.

• It is sensitive to extreme values.

• Because infinite number of distributions can have different maximum and minimum values but the same range, it can be helpful to report the range as the \([x_{\text{min}},\ x_{\text{max}}]\). This approach conveys more information about the data.

• Example: the range of the variable mpg in the mtcars dataset is calculated in R using the range() function:

  range(mtcars$mpg)

  [1] 10.4 33.9

  • The output is a vector of two values representing the minimum and maximum values, respectively.

2.2 Interquartile Range (IQR)

• It is defined as the difference between the third quartile \((Q_3)\) and the first quartile \((Q_1)\);

\[ IQR = Q_3 - Q_1 \]

• \(IQR\) reflects the variability among the middle \(50\%\) of the observations:

  • If \(IQR\) is large, it inidicates a large amount of variability.

  • If \(IQR\) is small, it indicates a small amount of variability.

• The IQR is calculated in R using the IQR() function as follows:

  IQR(mtcars$mpg)

  [1] 7.375

Note

• The summary() function in R can be used to get the minimum, \(Q_1\), median, \(Q_3\), and maximum values of a variable. In addition, it provides the counts of missing values, if any.

• For example, the summary of the variable mpg in the mtcars dataset is obtained as follows:

  summary(mtcars$mpg)

     Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
    10.40   15.43   19.20   20.09   22.80   33.90 

2.3 Variance

• The variance measures the variability relative to the scatter of the observations about their mean.

2.3.1 Population variance

• Finite population variance \(\sigma^2\) is defined as the mean of the squared differences (i.e., deviations) between each observation and the population mean \((\mu)\):

\[ \sigma^2 =\displaystyle \frac{1}{N} \displaystyle \sum_{i=1}^{N} (x_i - \mu)^2 = \displaystyle \frac{1}{N} \Big (\displaystyle \sum_{i=1}^{N} x_i^2 - \frac {\displaystyle \big (\sum_{i=1}^{N} x_i \big)^2}{N} \Big) \]

2.3.2 Sample variance

• Sample variance \((s^2)\) is defined as the mean of the squared differences (i.e., deviations) between each observation and the sample mean \((\bar{x})\):

\[ s^2 =\displaystyle \frac{1}{n-1} \displaystyle \sum_{i=1}^{n} (x_i - \bar{x})^2 = \displaystyle \frac{1}{n-1} \Big (\displaystyle \sum_{i=1}^{n} x_i^2 - \frac {\displaystyle \big (\sum_{i=1}^{n} x_i \big)^2}{n} \Big) \]

• More detailed discussion on the sample variance formula is provided here.

• The sample variance is calculated in R using the var() function as follows:

  var(mtcars$mpg)

  [1] 36.3241

• The above value is the same if we calculate the variance manually using the above formula:

  n <- length(mtcars$mpg)
  mean_mpg <- mean(mtcars$mpg)
  sum((mtcars$mpg - mean_mpg)^2) / (n - 1)

  [1] 36.3241

Note

• The expression \(\displaystyle \sum_{i=1}^{N} (x_i - \mu)^2\) or \(\displaystyle \sum_{i=1}^{n}(x_i - \bar{x})^2\) is referred to as sum of squares \(SS\).

• The unit of the variance is the square of the units of the observations making interpretation difficult.

2.4 Standard Deviation

• The standard deviation \((s)\) is the square root of the variance.

2.4.1 Population standard deviation

\[ \sigma = \sqrt{\sigma^2} = \sqrt{\displaystyle \frac{1}{N} \displaystyle \sum_{i=1}^{N} (x_i - \mu)^2} \]

2.4.2 Sample standard deviation

\[ s = \sqrt{s^2} = \sqrt{\displaystyle \frac{1}{n-1} \displaystyle \sum_{i=1}^{n} (x_i - \bar{x})^2} \]

• The sample standard deviation is calculated in R using the sd() function as follows:

  sd(mtcars$mpg)

  [1] 6.026948

• The above value is the same if we take the square root of the sample variance:

  sqrt(var(mtcars$mpg))

  [1] 6.026948

Note

• The standard deviation is more interpretable than the variance because it has the original unit of the observations.

• Therefore, it is preferred as a measure of variability.

• Similar to the variance, the standard deviation measures how much the observations are scattered around the mean (i.e., the average difference of the observations from the mean), therefore:

  • A low value of the standard deviation implies that the observations are more concentrated around the mean (i.e., low variability).

  • A high value of the standard deviation implies that the observations are more scattered around the mean (i.e., high variability).

2.5 Coefficient of Variation

• Assume that we want to compare the variability of two or more variables.

• Although the standard deviation is an appropriate measure of variability, it is not suitable for making this comparison directly because the variables might have different units causing the means to differ substantially. This also applies even if the variables are measured in the same units but have different means (differences in the standard deviation might be due to differences in the means not due to differences in the variability).

• Therefore, a relative measure of variability is needed that is independent of the unit of measurement or the mean.

• The coefficient of variation \((CV)\) is defined as the ratio of the standard deviation to the mean expressed as a percentage:

\[ CV = \displaystyle \frac{s}{\bar{x}} \times (100) \% \]

• It is unitless and is independent of the mean.

Example B.6.1

• The mean and standard deviation of the glucose and cholesterol levels of 10 subjects are given below:

  • Glucose: \(\bar{x}_{\text{glucose}} = 120\) mg/dL, \(s_{\text{glucose}} = 15\) mg/dL

  • Cholesterol: \(\bar{x}_{\text{cholesterol}} = 200\) mg/dL, \(s_{\text{cholesterol}} = 20\) mg/dL

• The coefficient of variation for glucose and cholesterol levels can be calculated as follows:

  • \(CV_{\text{glucose}} = \displaystyle \frac{15}{120} \times 100\% = 12.5\%\)

  • \(CV_{\text{cholesterol}} = \displaystyle \frac{20}{200} \times 100\% = 10\%\)

• Based on the results, we can conclude that the cholesterol levels are less variable than the glucose levels (even though the standard deviation of cholesterol levels is higher than that of glucose levels).

• Using the standard deviation to compare the variability would have led to the opposite conclusion.

Exercise B.6.1

• Load the PimaIndiansDiabetes dataset.

  Which of the following variables has the highest variability??

  glucose pressure mass

2.6 Median Absolute Deviation (MAD)

• The standard deviation is based on the mean, so it is also sensitive to outliers.

• Median Absolute Deviation (MAD) is a more robust measure of variability than the standard deviation.

• It is calculated based on the median of the observations and is defined as the median of the absolute deviations of the observations from the median:

\[ \text{MAD} = \text{median}(|x_i - \text{median}(x)|) \]

Example B.6.2

• Calculate \(MAD\) for the following observations: \(2, 5, 6, 8, 15\).

• The median of the observations is \(6\).

• The absolute deviations from the median are \(|2-6| = 4\), \(|5-6| = 1\), \(|6-6| = 0\), \(|8-6| = 2\), and \(|15-6| = 9\).

• Arrange the absolute deviations in ascending order: \(0, 1, 2, 4, 9\).

• The median of the absolute deviations \(\text{MAD} = 2\).

MAD of normal distribution

• If the distribution of a variable is normal (i.e., Gaussian), the following relationships hold:

  • \(\sigma \approx 1.4826 \times \text{MAD}\)

  • \(\text{IQR} \approx 2 \times \text{MAD}\)

• MAD can be calculated in R using the mad() function as follows:

  mad(c(2, 5, 6, 8, 15))

  [1] 2.9652

  • The result \((2.9652)\) is different from our manual calculation \((2)\) because the mad() function in R scales the \(\text{MAD}\) by a constant factor of \(1.4826\) for a normal distribution \((2 \times 1.4826 = 2.9652)\).

3 References

• Daniel, W. W. and Cross, C. L. (2013). Biostatistics: A Foundation for Analysis in the Health Sciences, Tenth edition. Wiley

• Heumann, C., Schomaker, M., and Shalabh (2022). Introduction to Statistics and Data Analysis: With Exercises, Solutions and Applications in R. Springer

• Hoffman, J. (2019). Basic Biostatistics for Medical and Biomedical Practitioners, Second Edition. Academic Press

• Lane, D. M. et al., (2019). Introduction to Statistics. Online Edition. Retrieved September 14, 2024, from https://openstax.org/details/introduction-statistics

4 Add your comments