Boxplot

1 Introduction

• A boxplot is used to graphically represent the distribution of numerical and ordinal data.

• In addition, it is helpful in identifying outliers.

2 Components of boxplot

• It consists of a box and two vertical lines (whiskers) extending from the box.

• For example, consider the following two boxplots:

  

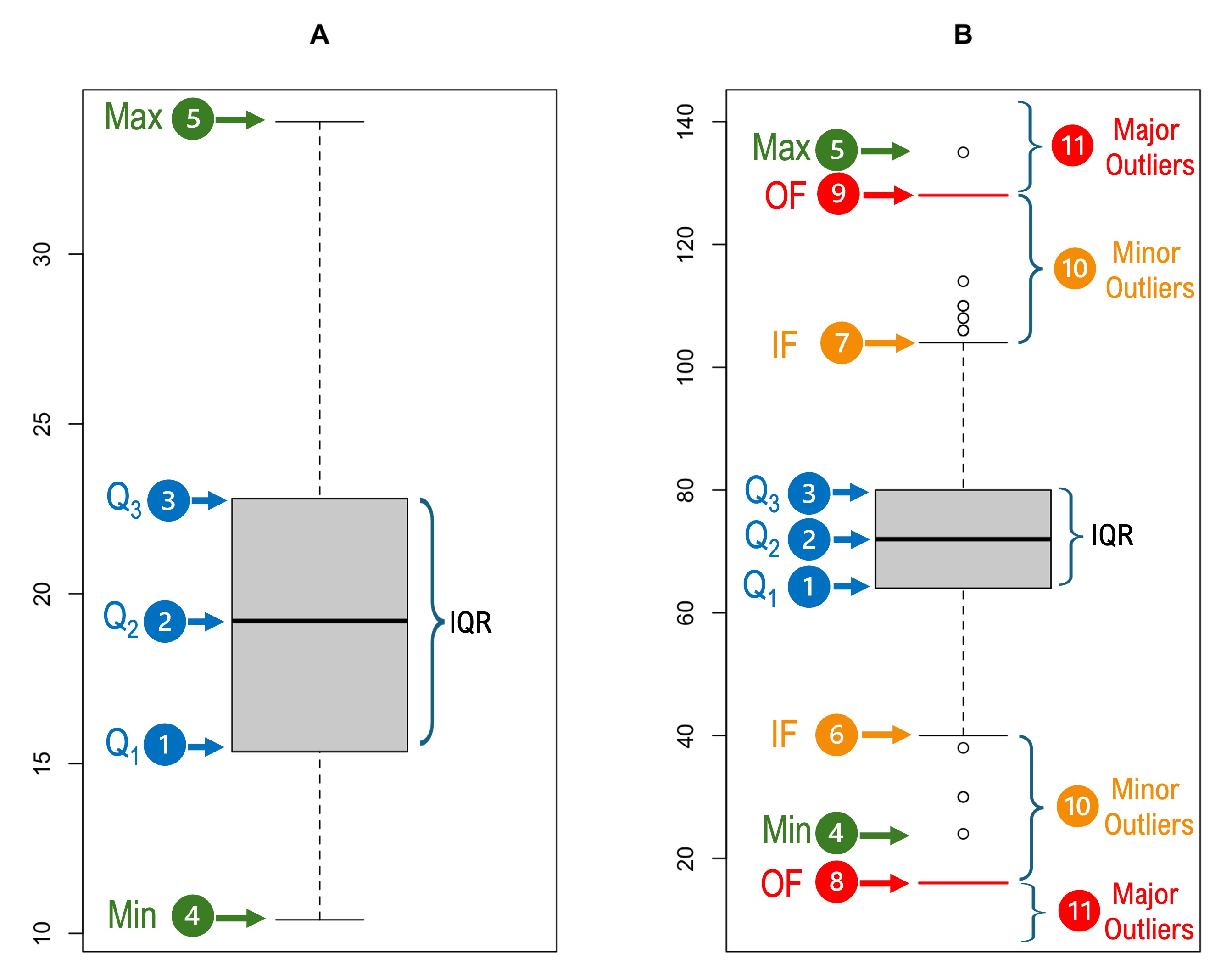
  • The Box:

    • It has has three horizontal lines (hinges).

      1. The bottom line represents the \(25^{th}\) percentile (first quartile, \(Q_1\)).

      2. The middle line represents the \(50^{th}\) percentile (median, \(Q_2\)).

      3. The top line represents the \(75^{th}\) percentile (third quartile, \(Q_3\)).

    IQR

    • The difference between the \(Q_3\) and \(Q_1\) is referred to as the `interquartile range (IQR)’, which is a measure of the spread of the middle \(50\%\) of the data and will be discussed later under the measures of dispersion.

  • The Whiskers:

    • The whiskers extend from the box to the minimum and maximum if they are contained within \(Q1 - (1.5 \times \text{IQR})\) and \(Q3 + (1.5 \times \text{IQR})\) as shown in the boxplot \(A\) to the left panel.

    • On the other hand, the whiskers are capped by short horizontal lines and (inner fences, IF) at \(Q1 - (1.5 \times \text{IQR})\) and \(Q3 + (1.5 \times \text{IQR})\) if there are values outside this range as shown in the boxplot \(B\) to the right panel. These fences are also referred to as Tukey’s fences.

    • Additionally, the boxplot \(B\) shows short horizontal lines and that are referred to as outer fences (OF) and are located at \(Q1 - (3 \times \text{IQR})\) and \(Q3 + (3 \times \text{IQR})\). However, the outer fences are not shown on the boxplot by default in R.

  • Outliers:

    • Grubbs defined outlier as “an observation that deviates markedly from other members of the sample in which it occurs.”

    • The values located between the inner and outer fences are termed minor outliers (Boxplot \(B\)).

    • The values located beyond the outer fences are termed major outliers (Boxplot \(B\)).

    • The function identify_outliers() from the rstatix package can be used to identify outliers based on Tukey’s method

3 Creating Boxplots in R

• As an example, we will use the pressure variable from the PimaIndiansDiabetes dataset which is available in the mlbench package or Sepal.Width variable from the iris dataset, which is available in base R.

• So, the first step is to load the required libraries and datasets:

  library(mlbench)
  data(PimaIndiansDiabetes)
  data(iris)

Base R

• The following figure shows the default boxplot in R with the fences at \(Q1 - (1.5 \times \text{IQR})\) and \(Q3 + (1.5 \times \text{IQR})\).

boxplot(
  PimaIndiansDiabetes$pressure, 
  range = 1.5,
  main = "Boxplot of the diastolic blood pressure",
  ylab = "Diastolic blood pressure (mm Hg)"
)

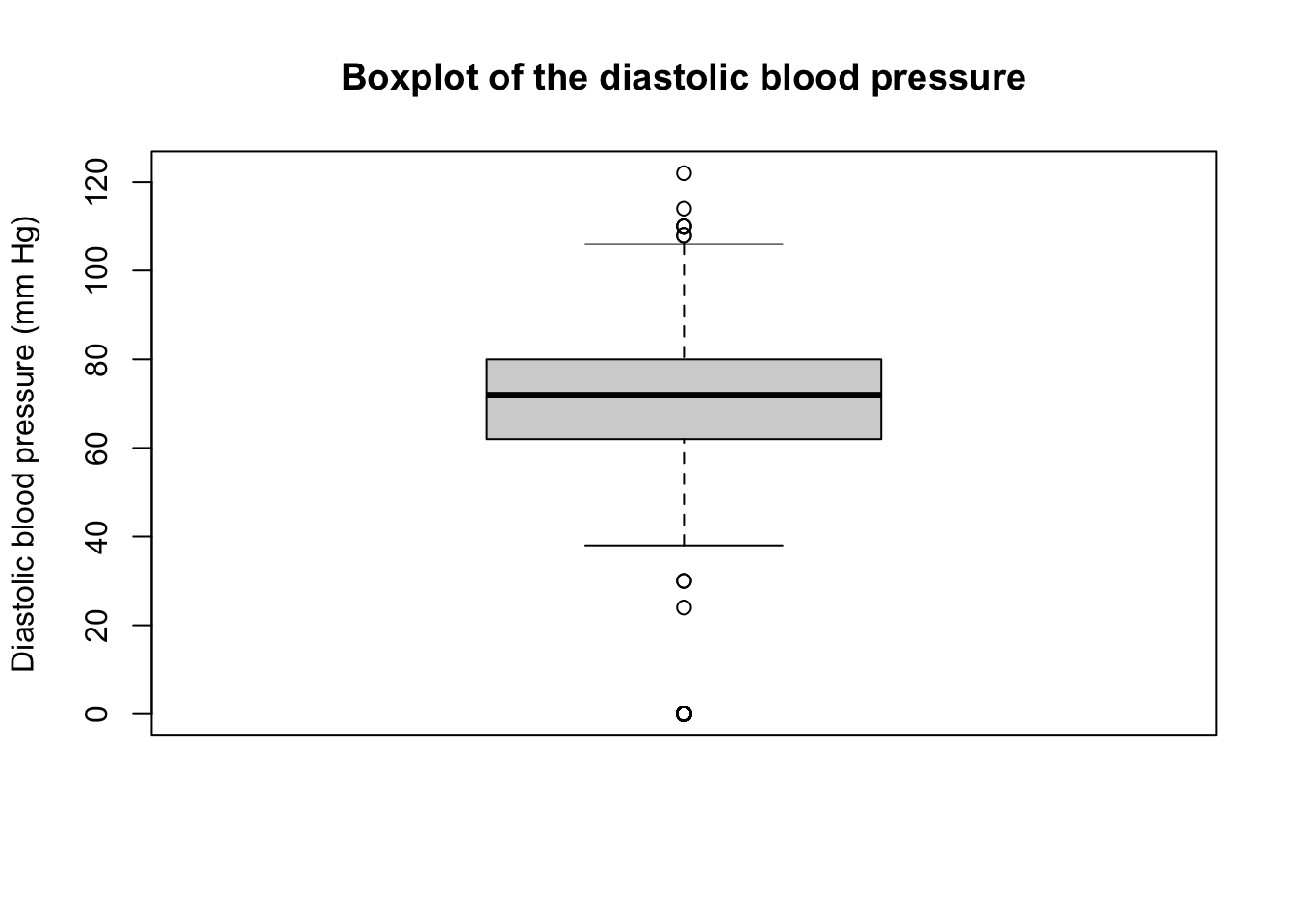
• The outlying observation can be identified using the function identify_outliers() from the rstatix package as follows:

  library(rstatix)

  
  Attaching package: 'rstatix'

  The following object is masked from 'package:stats':
  
      filter

  PimaIndiansDiabetes %>%
    select(pressure) %>%
    identify_outliers()

      pressure is.outlier is.extreme
  8          0       TRUE       TRUE
  16         0       TRUE       TRUE
  19        30       TRUE      FALSE
  44       110       TRUE      FALSE
  50         0       TRUE       TRUE
  61         0       TRUE       TRUE
  79         0       TRUE       TRUE
  82         0       TRUE       TRUE
  85       108       TRUE      FALSE
  107      122       TRUE      FALSE
  126       30       TRUE      FALSE
  173        0       TRUE       TRUE
  178      110       TRUE      FALSE
  194        0       TRUE       TRUE
  223        0       TRUE       TRUE
  262        0       TRUE       TRUE
  267        0       TRUE       TRUE
  270        0       TRUE       TRUE
  301        0       TRUE       TRUE
  333        0       TRUE       TRUE
  337        0       TRUE       TRUE
  348        0       TRUE       TRUE
  358        0       TRUE       TRUE
  363      108       TRUE      FALSE
  427        0       TRUE       TRUE
  431        0       TRUE       TRUE
  436        0       TRUE       TRUE
  454        0       TRUE       TRUE
  469        0       TRUE       TRUE
  485        0       TRUE       TRUE
  495        0       TRUE       TRUE
  523        0       TRUE       TRUE
  534        0       TRUE       TRUE
  536        0       TRUE       TRUE
  550      110       TRUE      FALSE
  590        0       TRUE       TRUE
  598       24       TRUE      FALSE
  602        0       TRUE       TRUE
  605        0       TRUE       TRUE
  620        0       TRUE       TRUE
  644        0       TRUE       TRUE
  692      114       TRUE      FALSE
  698        0       TRUE       TRUE
  704        0       TRUE       TRUE
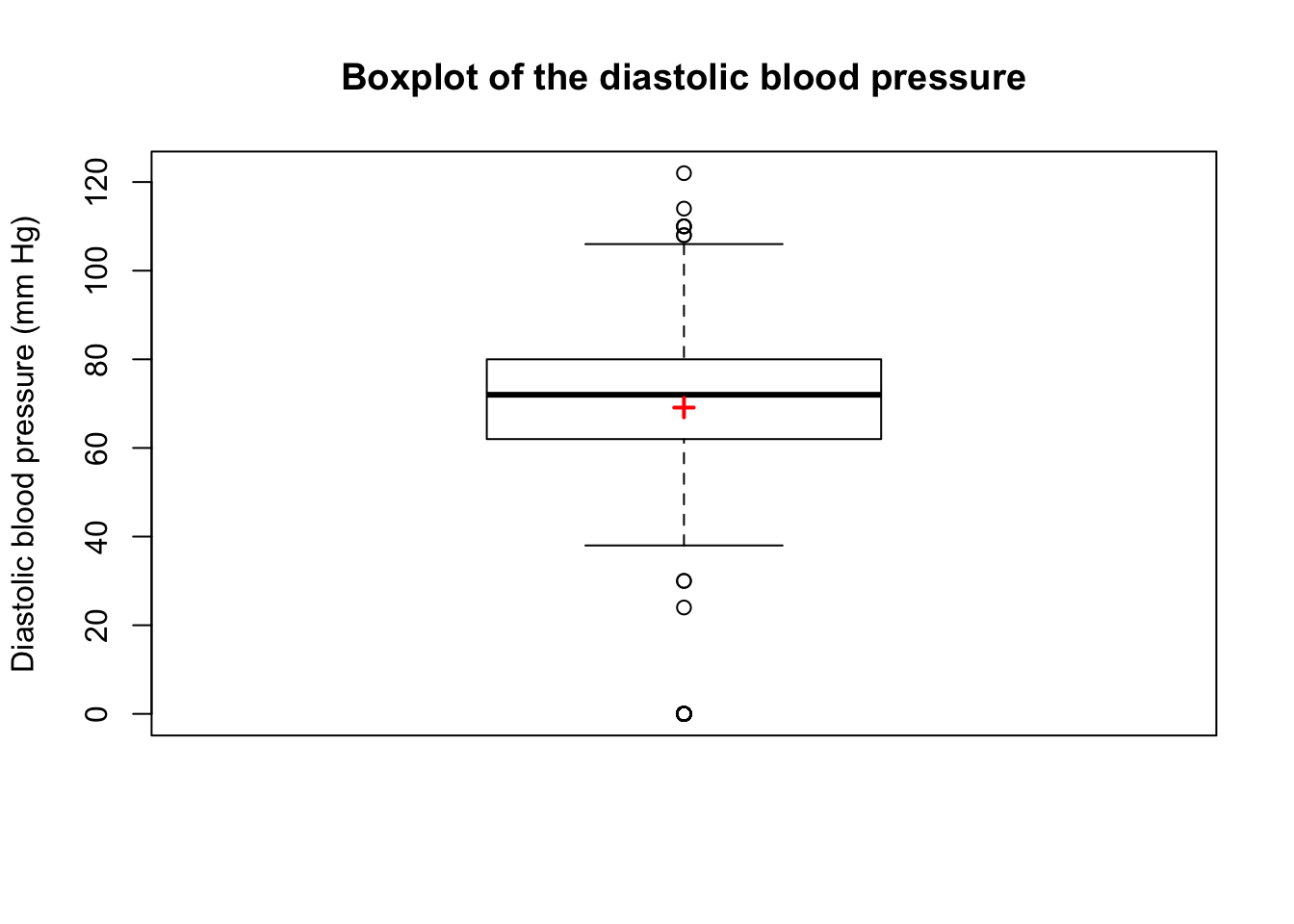
  707        0       TRUE       TRUE

  • The output shows the index and the value of the outlying observation and wether it is a minor (is.outlier) or major (is.extreme) outlier.

• A plus sign \((+)\) is sometimes drawn on the boxplot to indicate the mean as in the following figure:

boxplot(
  PimaIndiansDiabetes$pressure, 
  range = 1.5,
  main = "Boxplot of the diastolic blood pressure",
  ylab = "Diastolic blood pressure (mm Hg)",
  col = "white"
)

points(
  1, 
  mean(PimaIndiansDiabetes$pressure), 
  col = "red", 
  pch = 3, 
  cex = 1,
  lwd = 2
  
)

• Control fences location

  • The location of the fences can be controlled using the range argument:

    par(mfrow=c(1,3))
    
    boxplot(
      PimaIndiansDiabetes$pressure, 
      range = 1.5,
      main = "A \n Fences range = 1.5 (Default)"
    )
    
    boxplot(
      PimaIndiansDiabetes$pressure, 
      range = 3,
      main = "B \n Fences range = 3"
    )
    
    boxplot(
      PimaIndiansDiabetes$pressure,
      range = 0,
      main = "C \n Fences range = 0"
    )

    

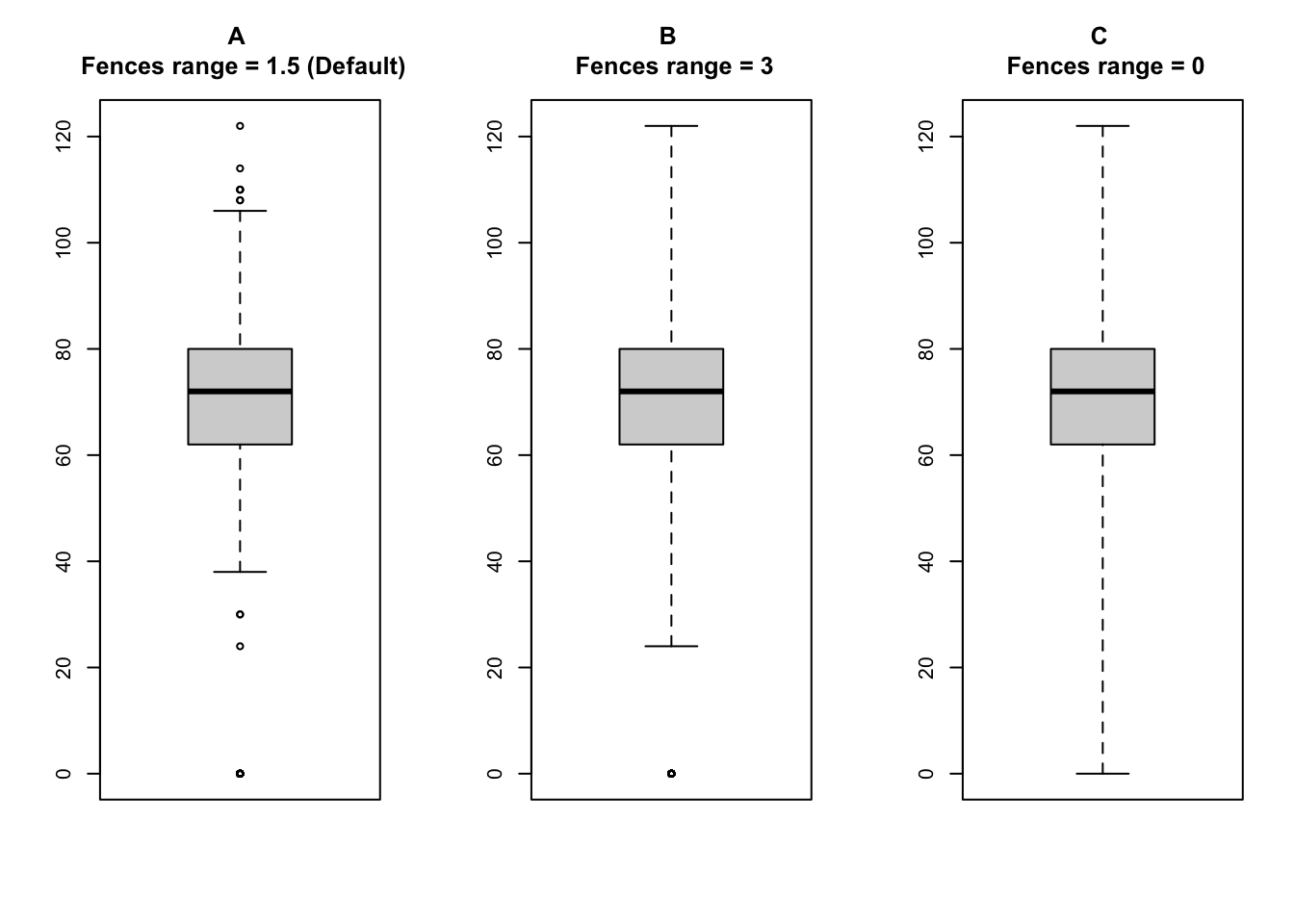
    • Figure \(A\) shows the boxplot with the fences at \(Q1 - (1.5 \times \text{IQR})\) and \(Q3 + (1.5 \times \text{IQR})\), which is the default setting in R.

    • Figure \(B\) shows the boxplot with the fences at \(Q1 - (3 \times \text{IQR})\) and \(Q3 + (3 \times \text{IQR})\).

    • Figure \(C\) shows the boxplot with the fences at the minimum and maximum values.

• Notch

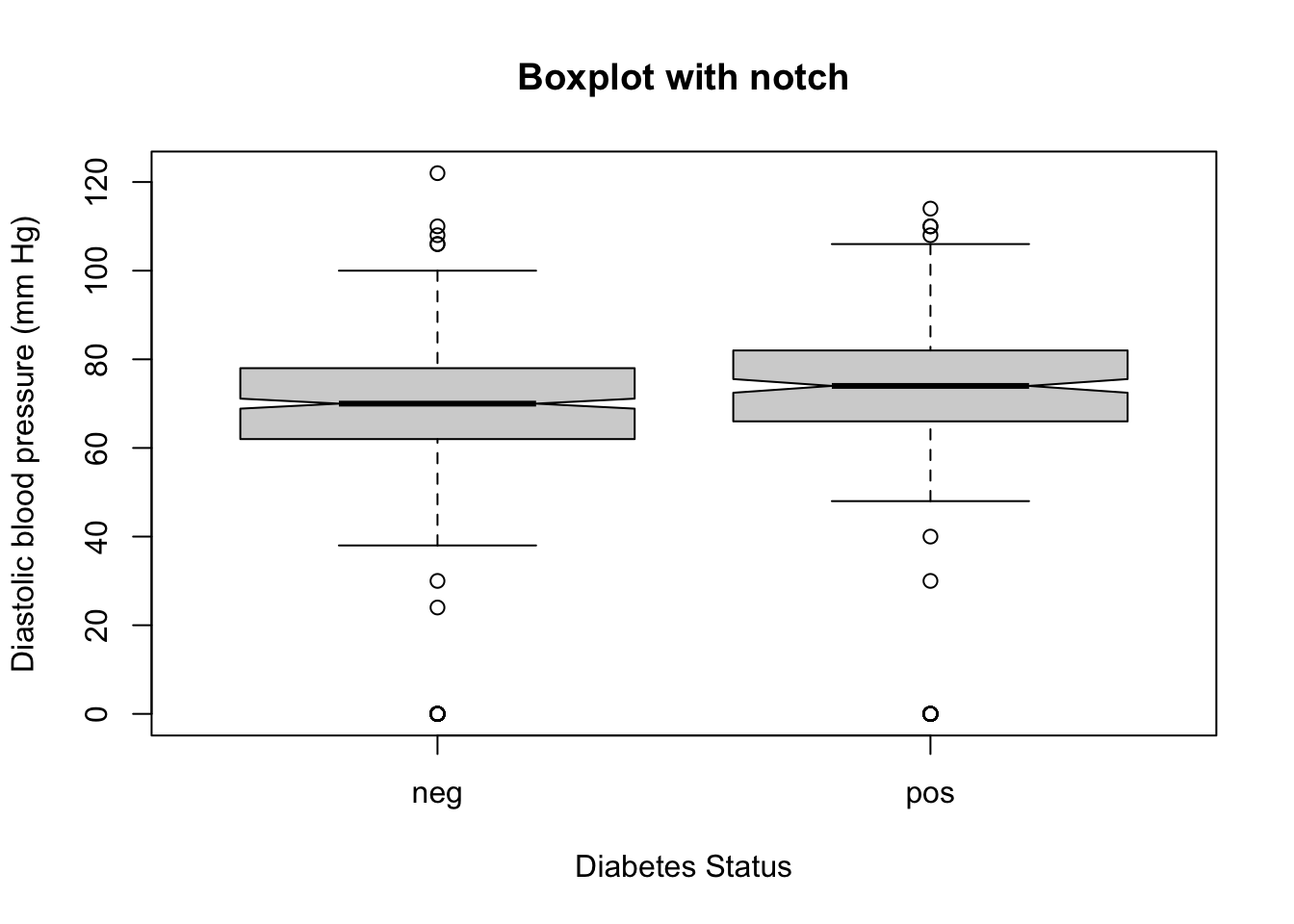
  • The notches in a boxplot represent a rough estimate of the confidence interval around the median.

  • They extend to the median \(\pm\ 1.58 \times \text{IQR}/ \sqrt{n}\).

  • Notches can be requested by setting the notch argument to TRUE.

  • The notches allow for the visual comparison of medians between two groups. If the notches of two boxplots do not overlap, it suggests that there is a statistically significant difference between the medians of the two groups at approximately the 95% confidence level. Conversely, if the notches overlap, the medians are not significantly different.

  • This is quoted from the help of boxplot.stats() “The notches (if requested) extend to \(\pm 1.58 IQR/sqrt(n)\). This seems to be based on the same calculations as the formula with 1.57 in Chambers et al. (1983, p. 62), given in McGill et al. (1978, p. 16). They are based on asymptotic normality of the median and roughly equal sample sizes for the two medians being compared, and are said to be rather insensitive to the underlying distributions of the samples. The idea appears to be to give roughly a 95% confidence interval for the difference in two medians.”

  • For example, the following code will draw boxplot with notches for the pressure variable from the PimaIndiansDiabetes dataset grouped by diabetes status:

        boxplot(
          pressure ~ diabetes,
          data = PimaIndiansDiabetes,
          notch = TRUE,
          main = "Boxplot with notch",
          xlab = "Diabetes Status",
          ylab = "Diastolic blood pressure (mm Hg)"
        )

    

    • The notches of the two boxes do not overlap, indicating that the medians are significantly different between the two groups (this can be confirmed by a formal statistical test such as Mood’s median test).

• Box width

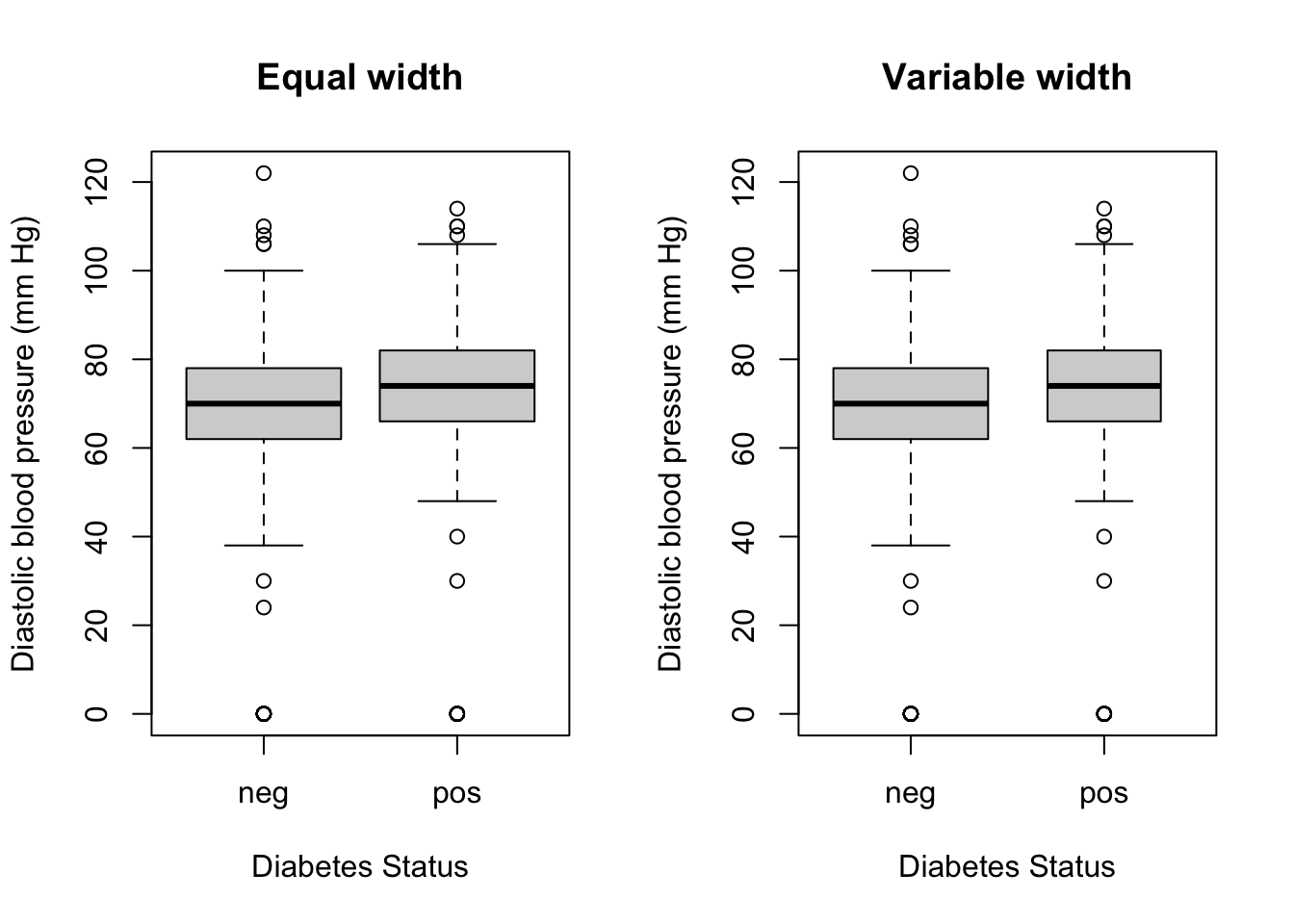
  • The argument varwidth can be set to TRUE to draw the boxes with widths proportional to the square root of the number of observations in the groups.

  • For example, the following code will draw boxplot with variable width for the pressure variable from the PimaIndiansDiabetes dataset grouped by diabetes status:

    par(mfrow=c(1,2)) 
    
    boxplot(
    PimaIndiansDiabetes$pressure ~ PimaIndiansDiabetes$diabetes,
    varwidth = FALSE,
    main = "Equal width",
    xlab = "Diabetes Status",
    ylab = "Diastolic blood pressure (mm Hg)"
    )
    
    boxplot(
    PimaIndiansDiabetes$pressure ~ PimaIndiansDiabetes$diabetes,
    varwidth = TRUE,
    main = "Variable width",
    xlab = "Diabetes Status",
    ylab = "Diastolic blood pressure (mm Hg)"
    )

    

ggplot2

library(ggplot2)
ggplot(
  data = PimaIndiansDiabetes,
  aes(
    x = diabetes, 
    y = pressure
  )
) +
  geom_boxplot(
    width = 0.5,
    color = "#0466c8",
    outlier.colour = "#e63946", 
    staplewidth = 0.2  # width of the horizontal lines relative to the box
  ) +
  stat_summary(
    fun = mean, 
    geom = "point", 
    shape = 3, 
    color = "red",
    size = 3
  ) +
  labs(
    x = "Diabetes Status",
    y = "Diastolic blood pressure (mm Hg)",
  ) +
  theme_bw()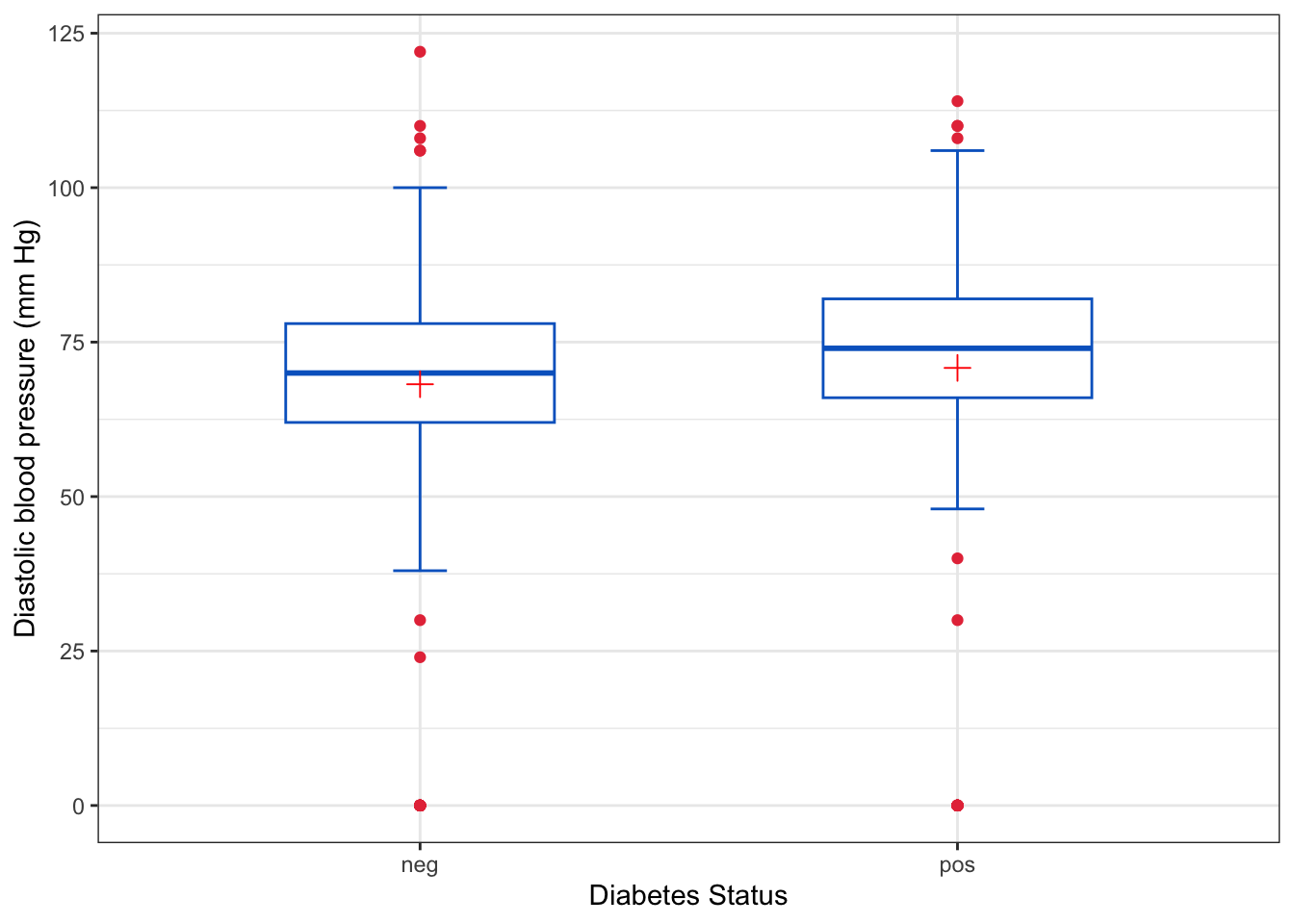

car

• The Boxplot function from the car package labels the outliers with the corresponding observation numbers.

  library(car)
  Boxplot(iris$Sepal.Width,
      main = "Boxplot of Sepal Width",
      xlab = "Iris Species",
      ylab = "Sepal Width"
  )

  

  [1] 61 16 33 34

• Observations \(61, 16, 33\) and \(34\) are considered as outliers.

4 Boxplots by base R vs. ggplot2

• The boxplot() function from base R and geom_boxplot() function from ggplot2 produce different boxplots because they are based on different algoriths for calculating quantiles.

• The following figure shows a side by side comparison of the boxplots produced by the two functions for the mpg variable from the mtcars dataset:

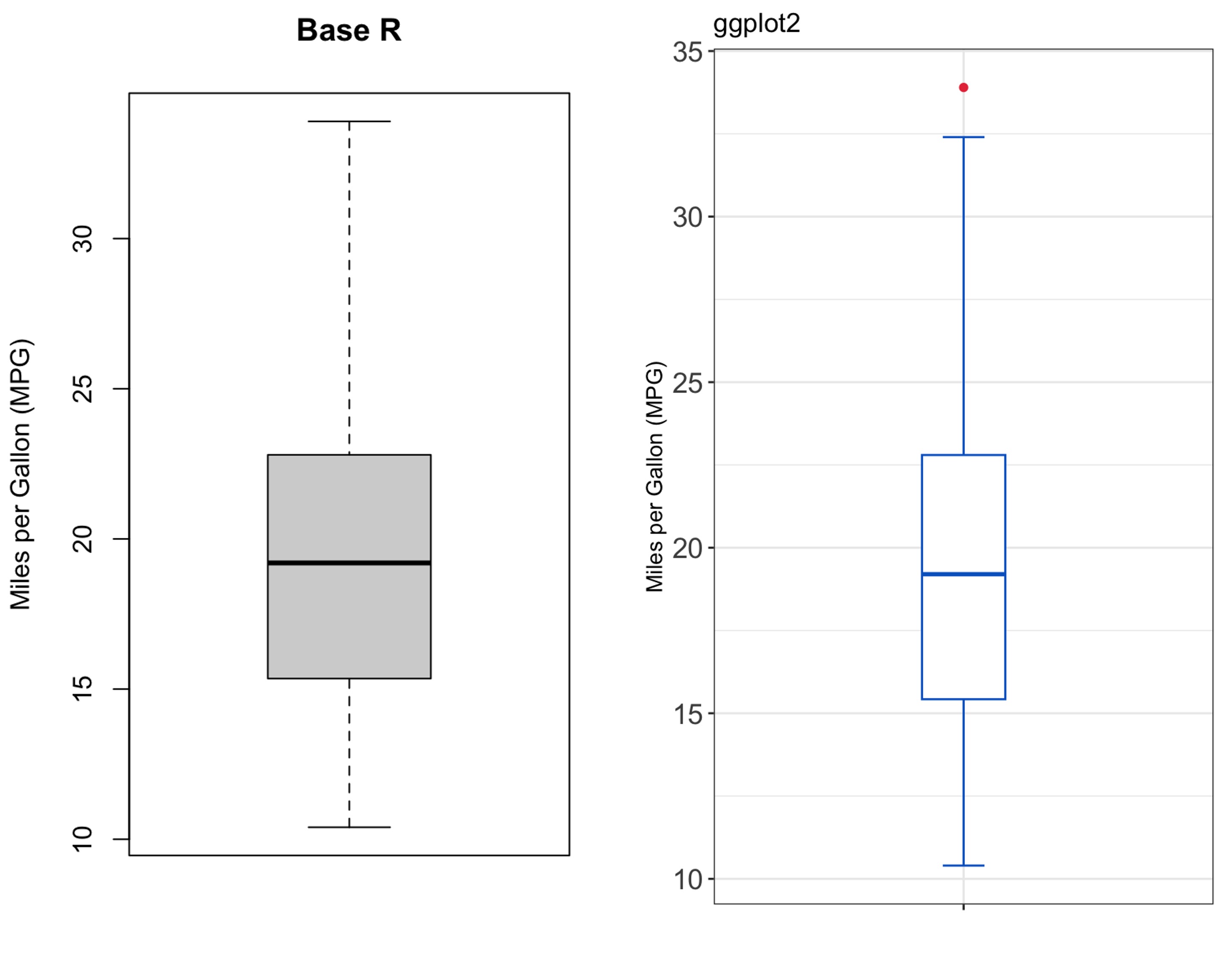
• As depicted in the figure, the boxplot produced by ggplot2 identifies one outlier that is not identified by the base R boxplot().

• To see the differences in calculations, we can extract the values used for constructing the boxplots using the boxplot.stats() function for base R and ggplot_build() function for ggplot2 as follows:

  boxplot.stats(mtcars$mpg)

  $stats
  [1] 10.40 15.35 19.20 22.80 33.90
  
  $n
  [1] 32
  
  $conf
  [1] 17.11916 21.28084
  
  $out
  numeric(0)

  box_ggplot <- ggplot(
    data = mtcars,
    aes(y = mpg)
    ) +
    geom_boxplot() 
  
  
  ggplot_build(box_ggplot)$data[[1]]

    ymin  lower middle upper ymax outliers notchupper notchlower x flipped_aes
  1 10.4 15.425   19.2  22.8 32.4     33.9   21.25989   17.14011 0       FALSE
    PANEL group ymin_final ymax_final   xmin  xmax xid newx new_width weight
  1     1    -1       10.4       33.9 -0.375 0.375   1    0      0.75      1
    colour  fill alpha shape linetype linewidth
  1 grey20 white    NA    19    solid       0.5

  • The output shows different \(Q_1\), \(Q_3\), and consequently different IQR, fences and outliers.

  • In addition, the notches are different because the of different \(IQR\).

5 Distribution insights from boxplots

• Boxplots can provide information about the distribution of data.

• For example, consider the following boxplots:

  set.seed(123)
  x <- rnorm(1000)
  y <- rexp(1000)
  
  par(mfrow=c(2, 2))
  plot(density(x), main="Density Plot of X")
  plot(density(y), main="Density Plot of Y")
  boxplot(x, main="Boxplot of X", col = "white")
  points(1, mean(x), col="red", pch=3)
  boxplot(y, main="Boxplot of Y", col = "white")
  points(1, mean(y), col="red", pch=3)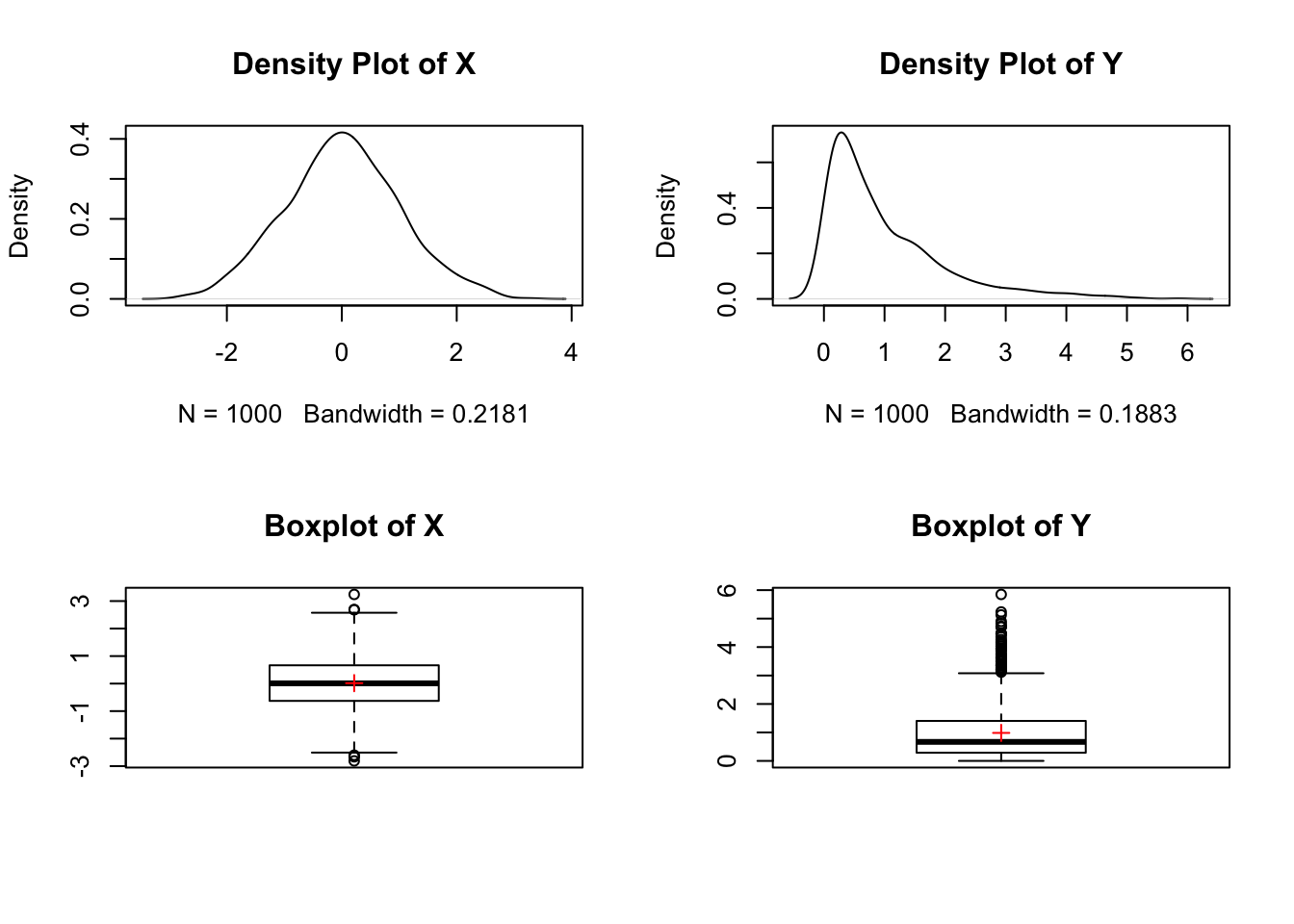

  

  • The boxplot of \(X\) is symmetric with the median at the center of the box, the whiskers are of equal length, and a few outliers on both sides of the whiskers. In addition, the mean and median appear to be identical.

  • On the other hand, the boxplot of \(Y\) is skewed to the right with the median closer to the \(Q_1\), the whisker on the right is longer than the whisker on the left with many outliers on the right side. The mean is greater than the median, which is due to the presence of outliers on the right side (right skewness).

6 Other variations of boxplots

• Boxplots can be misleading because they cannot capture the shape of the distribution accurately. For example, the fail to capture multimoality or kurtosis (i.e., peakedness of the distribution).

• Therefore, other variants of boxplots have been used by overlaying the original observations on the boxplot as jittered points or dot plots or wrapping the boxplot in a violin plot that shows the density of the data. These approaches provide more insights about the distribution of the data.

• Jittering means slightly displacing (spreading) the points horizontally to avoid overlapping, while in the dot plot, the points are stacked on top of each other.

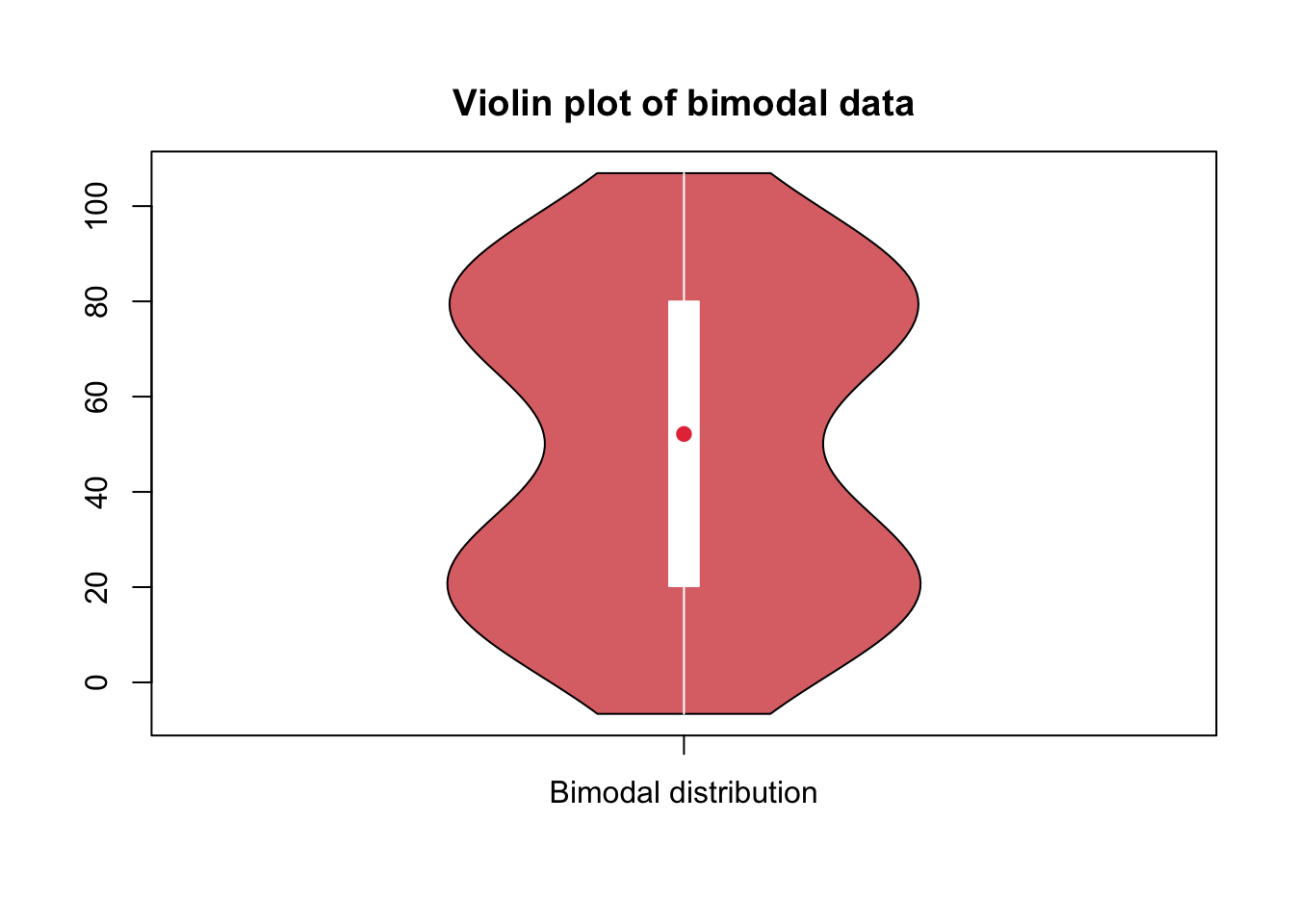
• The following figure shows that boxplot lacks the ability to capture the bimodal nature of the data, which is evident from the density plot or the boxplot with jittered points:

  # Load necessary libraries
  set.seed(123)
  
  # Generate Bimodal Data with clear separation
  data_bimodal <- c(
    rnorm(500, mean = 20, sd = 10), 
    rnorm(500, mean = 80, sd = 10)
  )
  
  
  par(mfrow=c(3,1))
  
  boxplot(
    data_bimodal, 
    main = "Boxplot of bimodal Data", 
    ylab = "Values", 
    horizontal = TRUE)
  
  plot(
    density(data_bimodal), 
    main = "Density Plot of bimodal Data"
  )
  
  boxplot(
    data_bimodal, 
    main = "Boxplot of bimodal Data",
    horizontal = TRUE,
    col = "white"
  )
  
  stripchart(
    data_bimodal,
    method = "jitter",
    pch = 19, # select the point type
    add = TRUE, # add the points to the existing plot
    col = "#0466c8",
    vertical = FALSE,
    jitter = 0.1 # control the amount of jittering
  )

  

  • Both the density plot and the boxplot with jittered points show bimodality as two peaks in the former and two distinct clusters in the latter, which are not captured by the standard boxplot.

6.1 Creating boxplot with jittered points

Base R

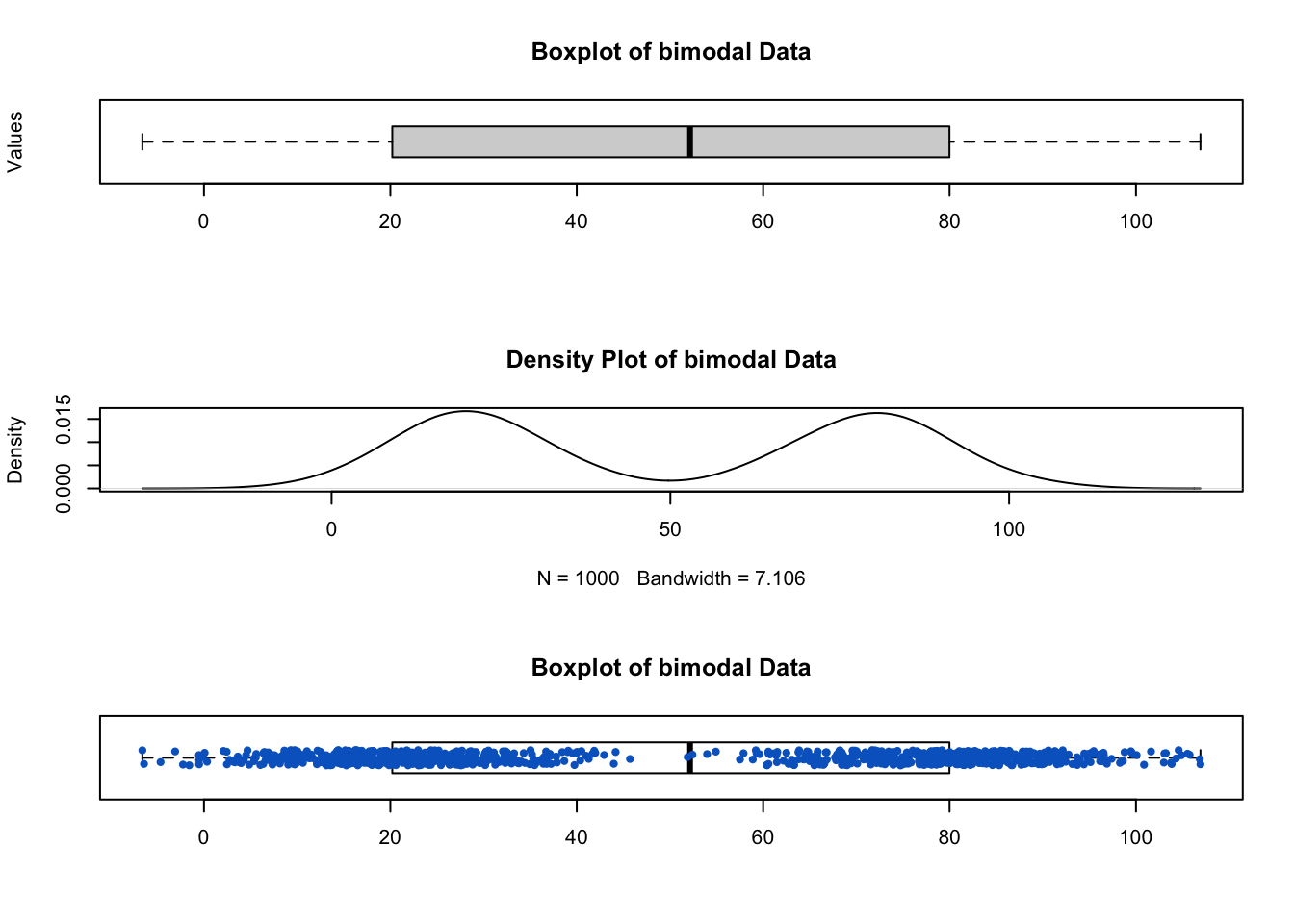
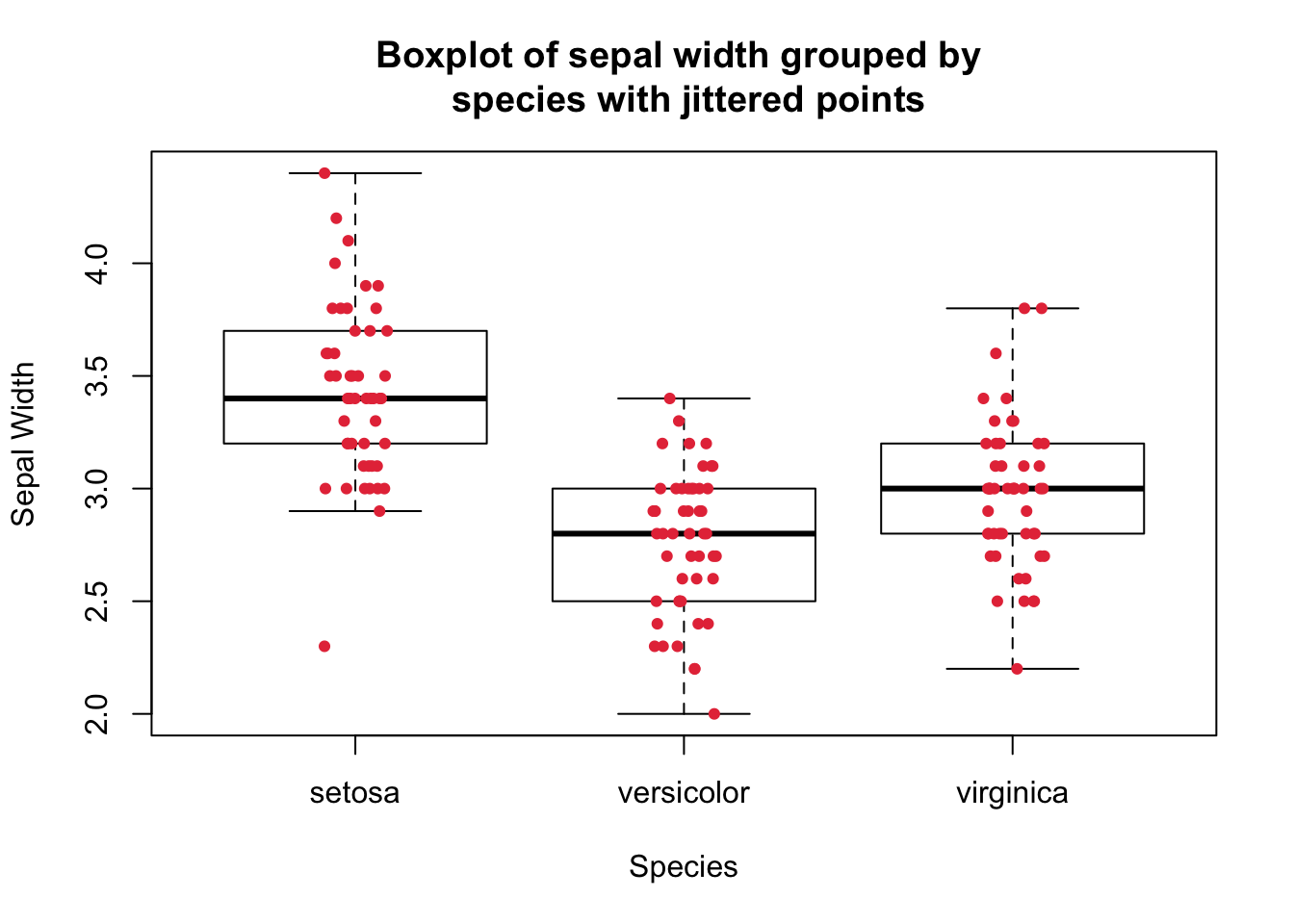
• Using stripchart() function to produce jittered points.

  boxplot(
    Sepal.Width ~ Species,
    data = iris,
    col = "white",
    outline = FALSE,
    main = "Boxplot of sepal width grouped by \n species with jittered points",
    xlab = "Species",
    ylab = "Sepal Width"
  )
  
  stripchart(
    Sepal.Width ~ Species,
    data = iris,
    method = "jitter",  # select the jitter method
    pch = 19,  # select the point type
    add = TRUE,  # add the points to the existing plot
    col = "#e63946", 
    vertical = TRUE, 
    jitter = 0.1,  # control the amount of jittering
    cex = 0.7  # control the size of the points
  )

  

ggplot2

library(ggplot2)
ggplot(
  data = iris,
  aes(
    x = Species,
    y = Sepal.Width
  )
) +
  geom_boxplot(
    width = 0.5,
    color = "#0466c8",
    outliers = FALSE,
    staplewidth = 0.2
  ) +
  geom_jitter(
    width = 0.2,
    color = "#e63946",
    size = 0.7
  ) +
  labs(
    x = "Sepal Width",
    y = "Species",
  ) +
  labs(title = "Boxplot with jittered points") +
  theme_bw()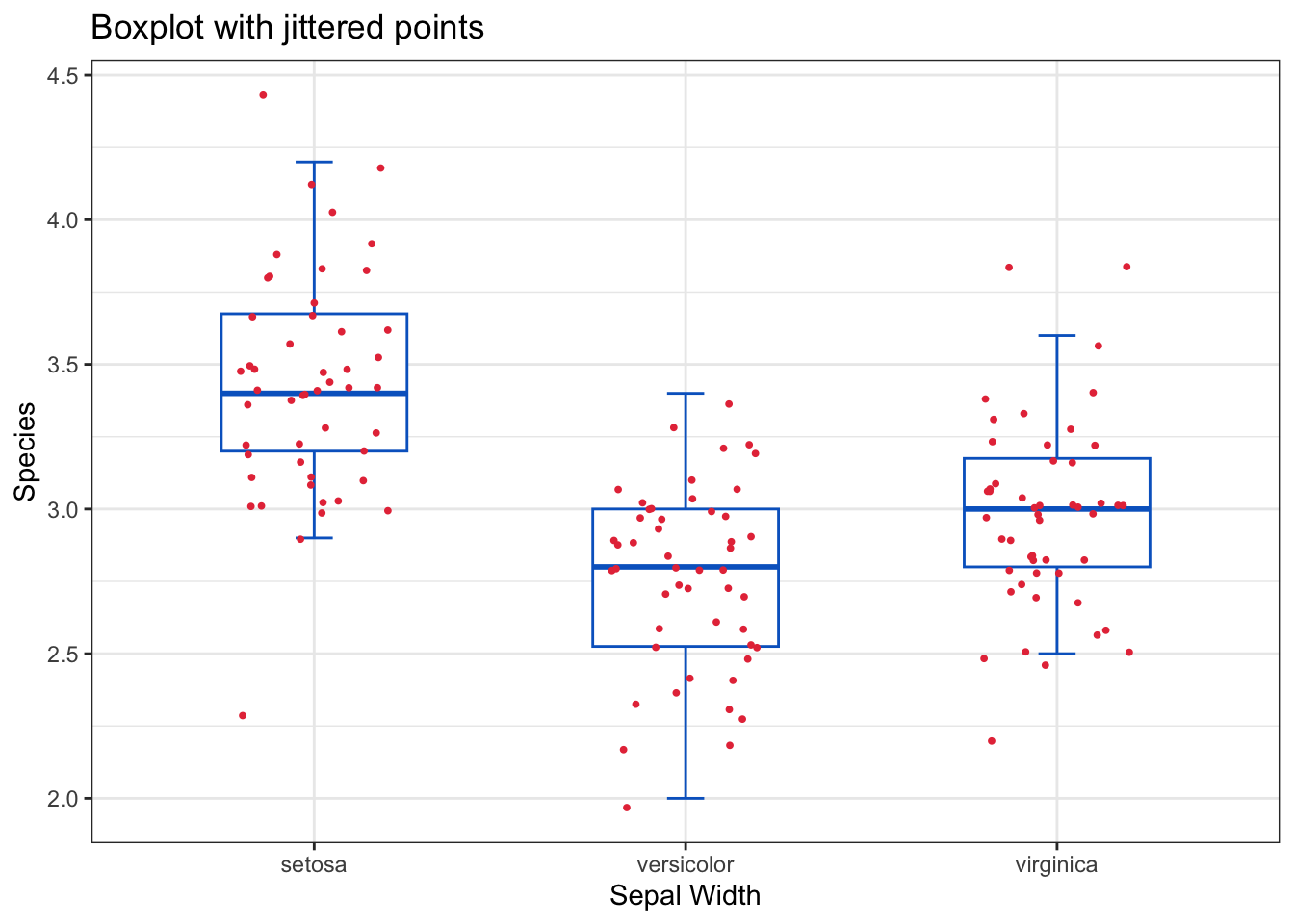

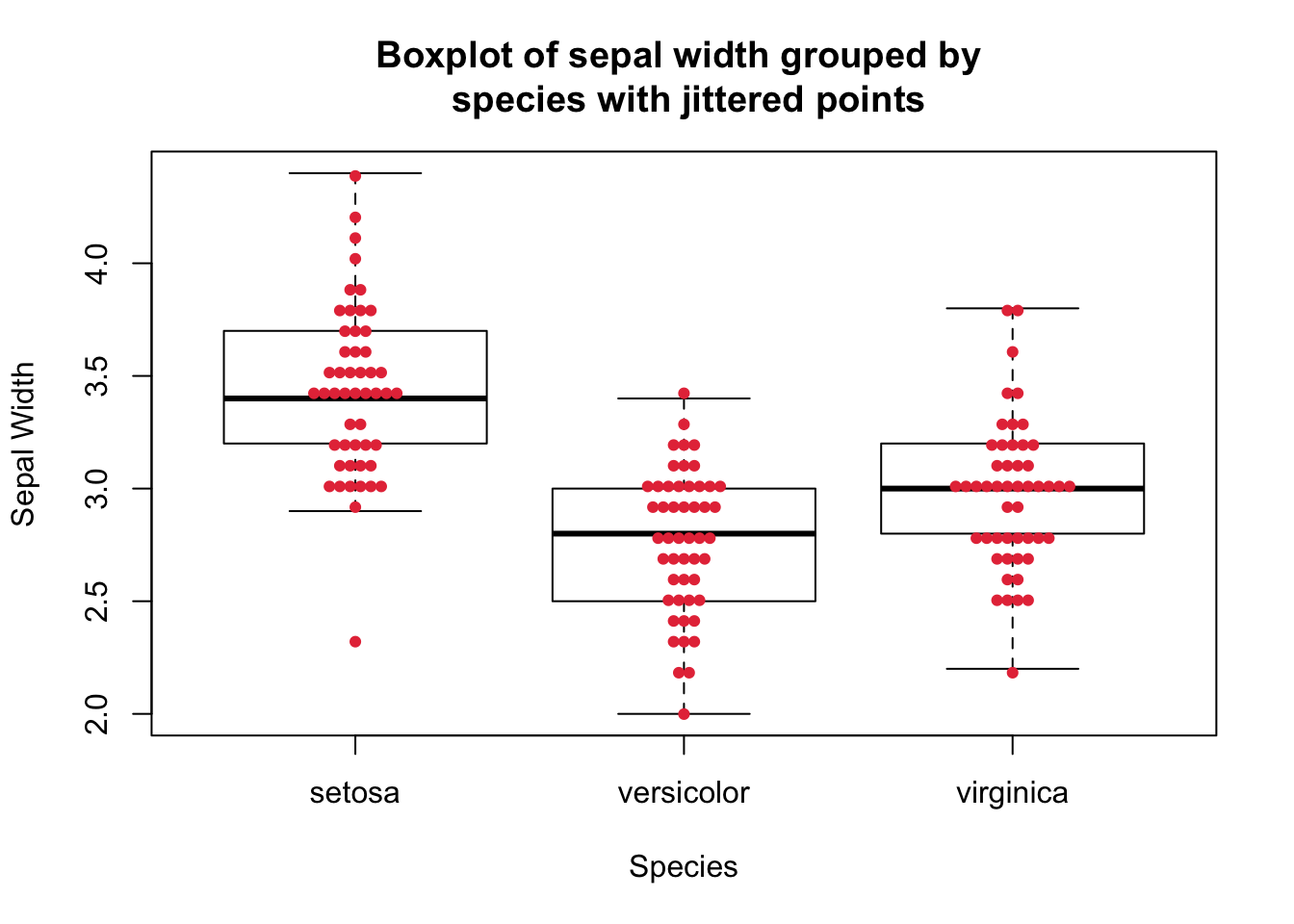
6.2 Creating boxplot with dot plot

Base R

• Using beeswarm function from the beeswarm package that provides various methods to separate coincident points such that the points are stacked and do not overlap.

library(beeswarm)

boxplot(
  Sepal.Width ~ Species,
  data = iris,
  col = "white",
  outline = FALSE,
  main = "Boxplot of sepal width grouped by \n species with jittered points",
  xlab = "Species",
  ylab = "Sepal Width"
)

beeswarm(
  Sepal.Width ~ Species,
  data = iris,
  pch = 19, # select the point type
  add = TRUE, # add the points to the existing plot
  col = "#e63946",
  method = "center", # select the jitter method
  cex = 0.7 # control the size of the points
)

ggplot2

ggplot(
  data = iris,
  aes(
    x = Species,
    y = Sepal.Width
  )
) +
  geom_boxplot(
    width = 0.5,
    color = "#0466c8",
    outliers = FALSE, 
    staplewidth = 0.2
  ) +
  geom_dotplot(
    binaxis = "y",
    stackdir = "center",
    dotsize = 0.4,
    fill = "#e63946",
    color = "#e63946",
  ) +
  labs(
    x = "Sepal Width",
    y = "Species",
  ) +
  labs(title = "Boxplot with dot plot") +
  theme_bw()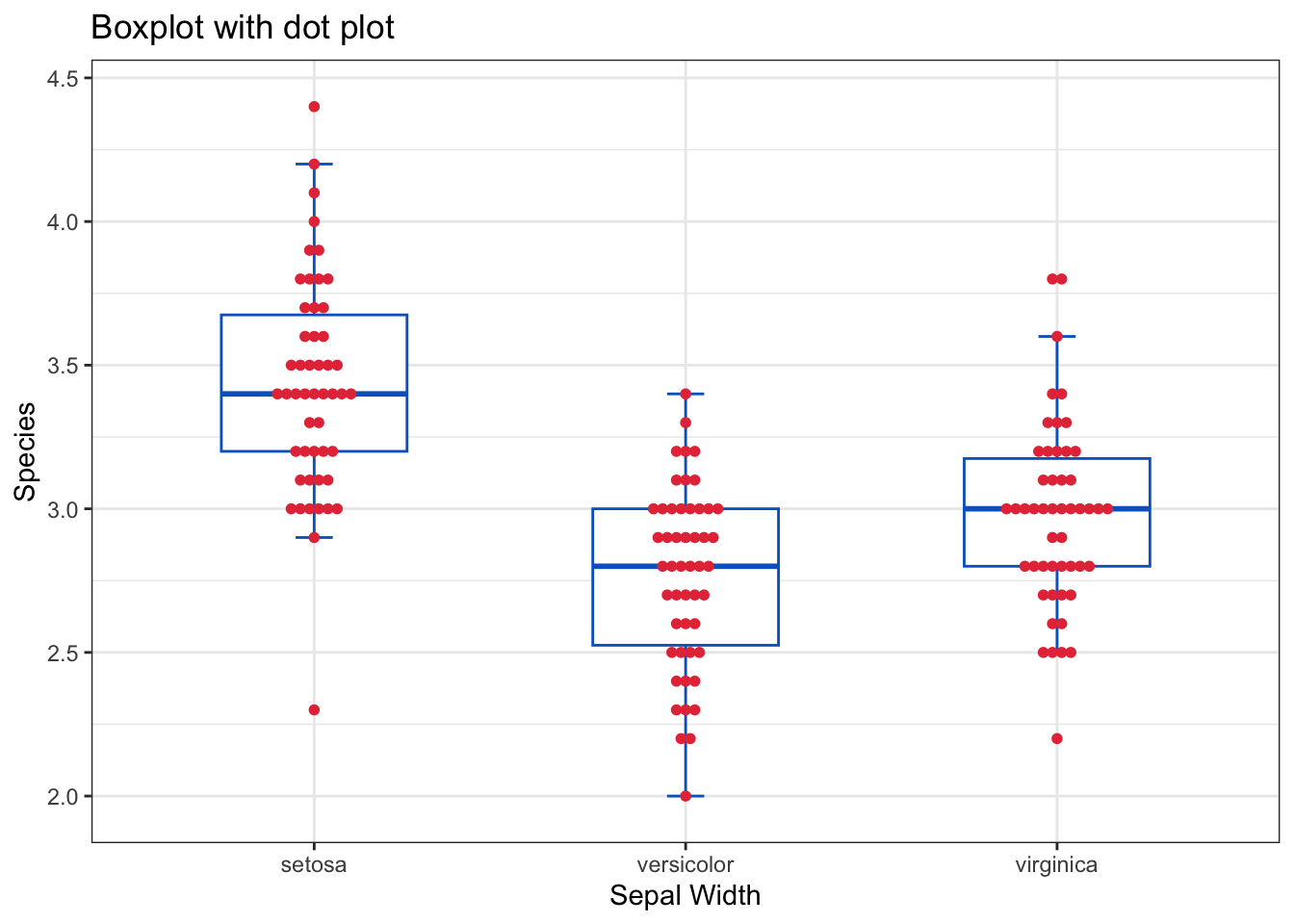

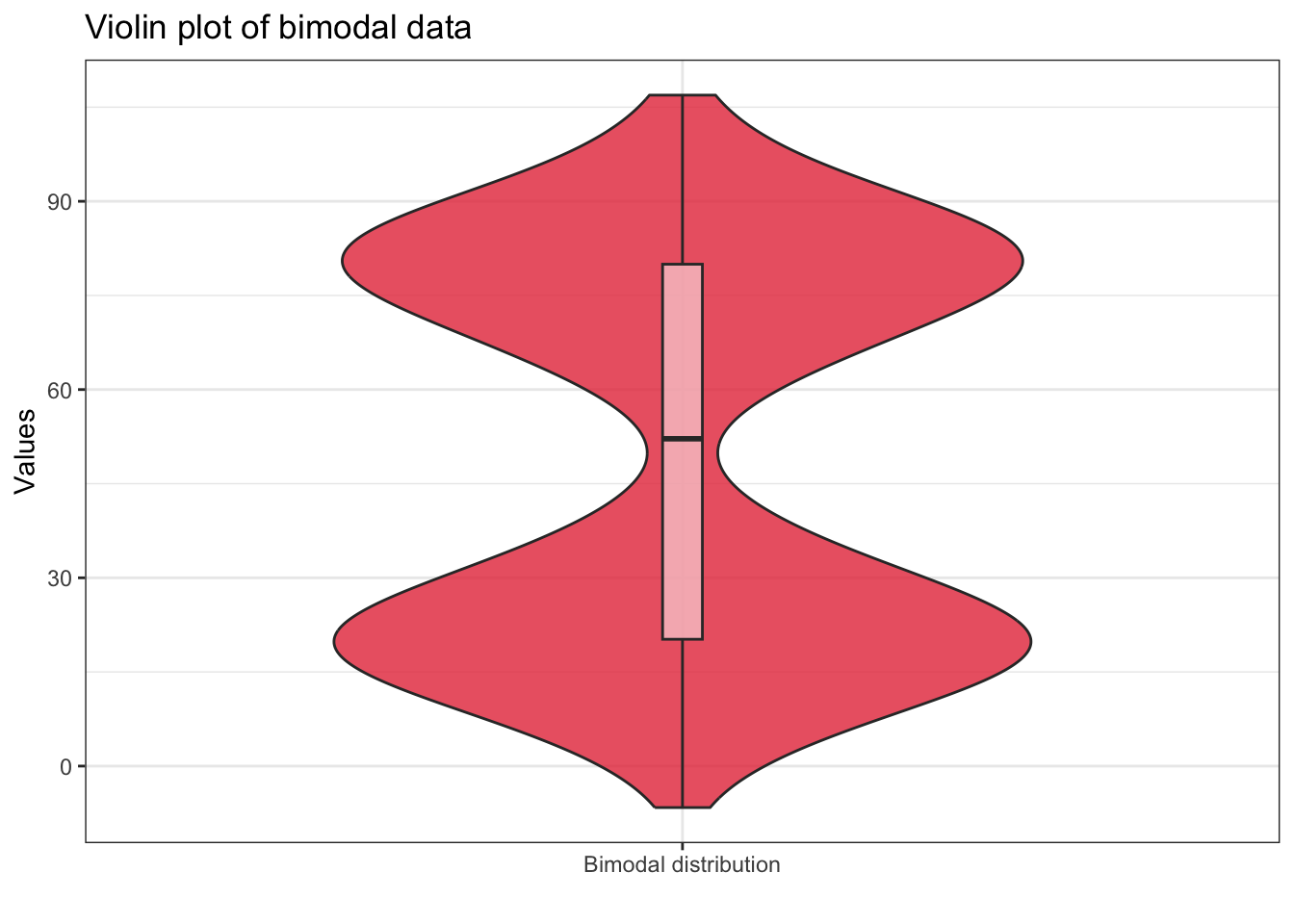
6.3 Creating boxplot wrapped in violin plot

Base R

library(vioplot)
vioplot(
  x = data_bimodal, 
  rectCol = "white",  # color of the box
  lineCol = "white",  # color of the lines
  colMed = "#e63946",  # color of the median point
  wex = 0.6,  # relative expansion of the violin 
  col = rgb(212/255, 73/255, 76/255, alpha = 0.8),
  names = "Bimodal distribution",  # label for variable
  main = "Violin plot of bimodal data"
  )

Using ggpubr

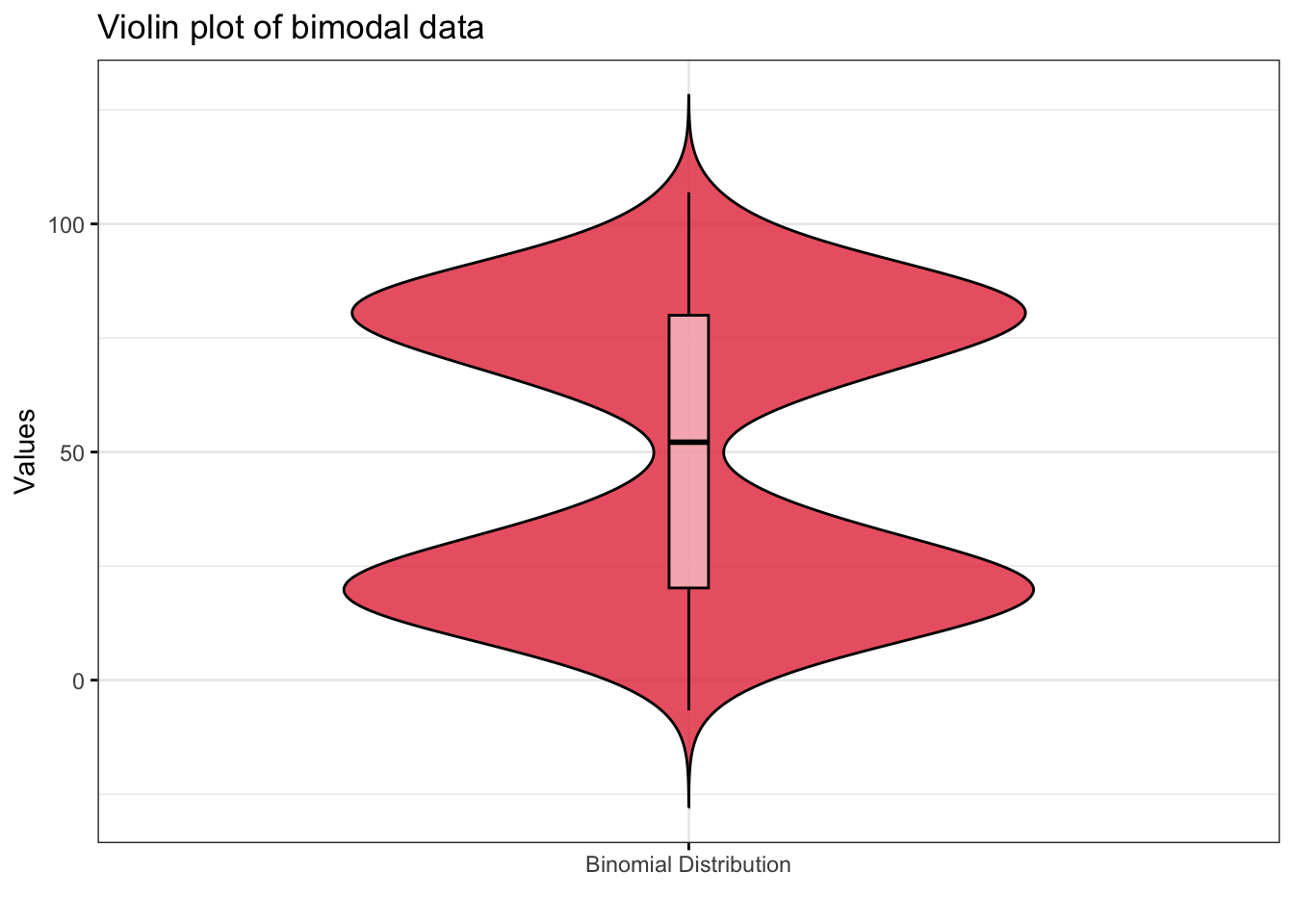
library(ggpubr)
my_data <- data.frame(
  x = data_bimodal,
  group = "Binomial Distribution"
)

ggviolin(
  data = my_data,
  x = "group",
  y = "x",
  fill = "#e63946",
  alpha = 0.8,
  width = 0.7,
  xlab = "",
  ylab = "Values",
  main = "Violin plot of bimodal data",
  add = "boxplot",
  add.params = list(
    alpha = 0.5,
    fill = "white",
    width = 0.04
  ),
  ggtheme = theme_bw()
)

ggplo2

ggplot(
  data = data.frame(x = data_bimodal),
  aes(x = "Bimodal distribution", y = x)
) +
  geom_violin(
    fill = "#e63946",
    alpha = 0.8,
    width = 0.7
  ) +
  geom_boxplot(
    fill = "white",
    alpha = 0.5,
    width = 0.04
  ) +
  labs(
    x = "",
    y = "Values"
  ) +
  labs(title = "Violin plot of bimodal data") +
  theme_bw()

7 References

• Daniel, W. W. and Cross, C. L. (2013). Biostatistics: A Foundation for Analysis in the Health Sciences, Tenth edition. Wiley

• Heumann, C., Schomaker, M., and Shalabh (2022). Introduction to Statistics and Data Analysis: With Exercises, Solutions and Applications in R. Springer

• Lane, D. M. et al., (2019). Introduction to Statistics. Online Edition. Retrieved September 14, 2024, from https://openstax.org/details/introduction-statistics

8 Add your comments