Describing the shape of distribution

Published

November 15, 2024

1 Background

  • The shape of a distribution can be described in terms of the direction and degree of asymmetry, measured by skewness, and the heaviness of the tails, measured by kurtosis.

2 Skewness

  • It is a measure of the direction and degree of asymmetry of a distribution.

  • It is described as the standardized third moment \((m_3)\) of the distribution about the mean (the concept of moments will be discussed in upcoming articles).

2.1 Formula

  • There are three formulas to calculate skewness (we will use sample moments):

    1. Raw formula \(g_1\):

      \[ g_1 = \displaystyle \frac{m_3}{m_2^{3/2}} \]

      • \(m_3\) is the third moment about the mean:

        \[ m_3 = \displaystyle \frac{1}{n} \sum_{i=1}^{n} (x_i - \bar{x})^3 \]

      • \(m_2\) is the second moment about the mean:

        \[ m_2 = \displaystyle \frac{1}{n} \sum_{i=1}^{n} (x_i - \bar{x})^2 \]

      • It is not biased-corrected for small samples.

      • This formula is used by Excel(SKEW.P function).

    2. Fisher’s \(G_1\):

      \[ G_1 = g_1 \displaystyle \frac{\sqrt {n(n-1)}}{n-2} \]

      • This measure of skewness is bias-corrected for small samples.

      • As \(n\) increases, the correction factor becomes closer to \(1\).

      • This formula is used by SAS, SPSS, NCSS, Excel (SKEW function), and Graphpad Prism.

    3. Skewness \(b_1\):

      \[ b_1 = \displaystyle \frac{m_3}{s^3} = g_1 \big (\displaystyle \frac{n-1}{n} \big)^{3/2} \]

      • \(s\) is the sample standard deviation \(\big [s = \sqrt{\displaystyle \frac{1}{n-1} \sum_{i=1}^{n} (x_i - \bar{x})^2} \big]\).

      • This formula is used by Minitab.

      • This measure uses a slight adjustment by including the factor \((\displaystyle \frac{n-1}{n})^{3/2}\).

  • The standard error of skewness is given by:

    \[ SE_{skewness} = \sqrt \frac{6n(n-1)}{(n-2)(n+1)(n+3)} \]

2.2 Interpretation

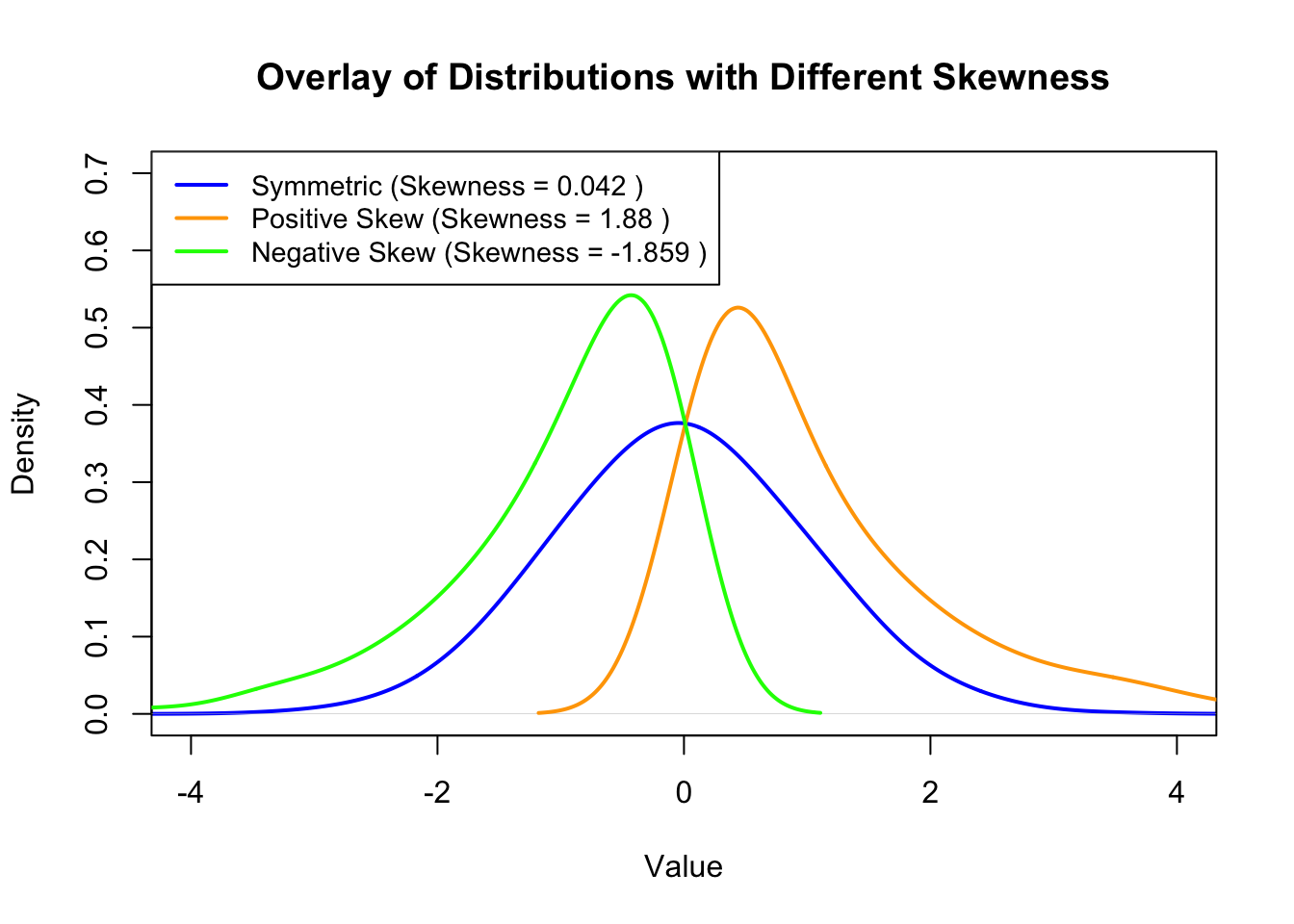
  • A skewness value of zero indicates a symmetrical distribution (mean and median are equal or approximately equal).

  • A positive value indicates a long right tail (right-skewed distribution, the mean is greater than the median).

  • A negative value indicates a long left tail (left-skewed distribution, the mean is less than the median).

  • Further interpretation will be discussed in detail under assessing the normality of data.

  • The following figure shows different distributions and their skewness values:

2.3 Calculation in R

  • Different functions in R can be used to calculate the skewness:

    • skewness() function from the moments package (uses formula 1).

    • Skewness() function from the sasLM package (uses formula 2).

    • skew() function from the psych package or skewness() function from the e1071 package can calculate skewness using the three formulas by setting the type argument to either \(1\), \(2\), or \(3\).

  • The skewness standard error can be calculated using the SkewnessSE() function from the sasLM package.

  • For example, the skewness of the insulin variable from the PimaIndiansDiabetes dataset can be calculated as follows:

    • First, let’s plot the density of the insulin variable:

      Click to show/hide code 
          # load the library and dataset
    library(mlbench)
    data(PimaIndiansDiabetes)

    # plot density of the insulin variable
    plot(
      density(PimaIndiansDiabetes$insulin, adjust =2),
      main = "Density plot of insulin",
      lwd = 2,
      col = "#0466c8",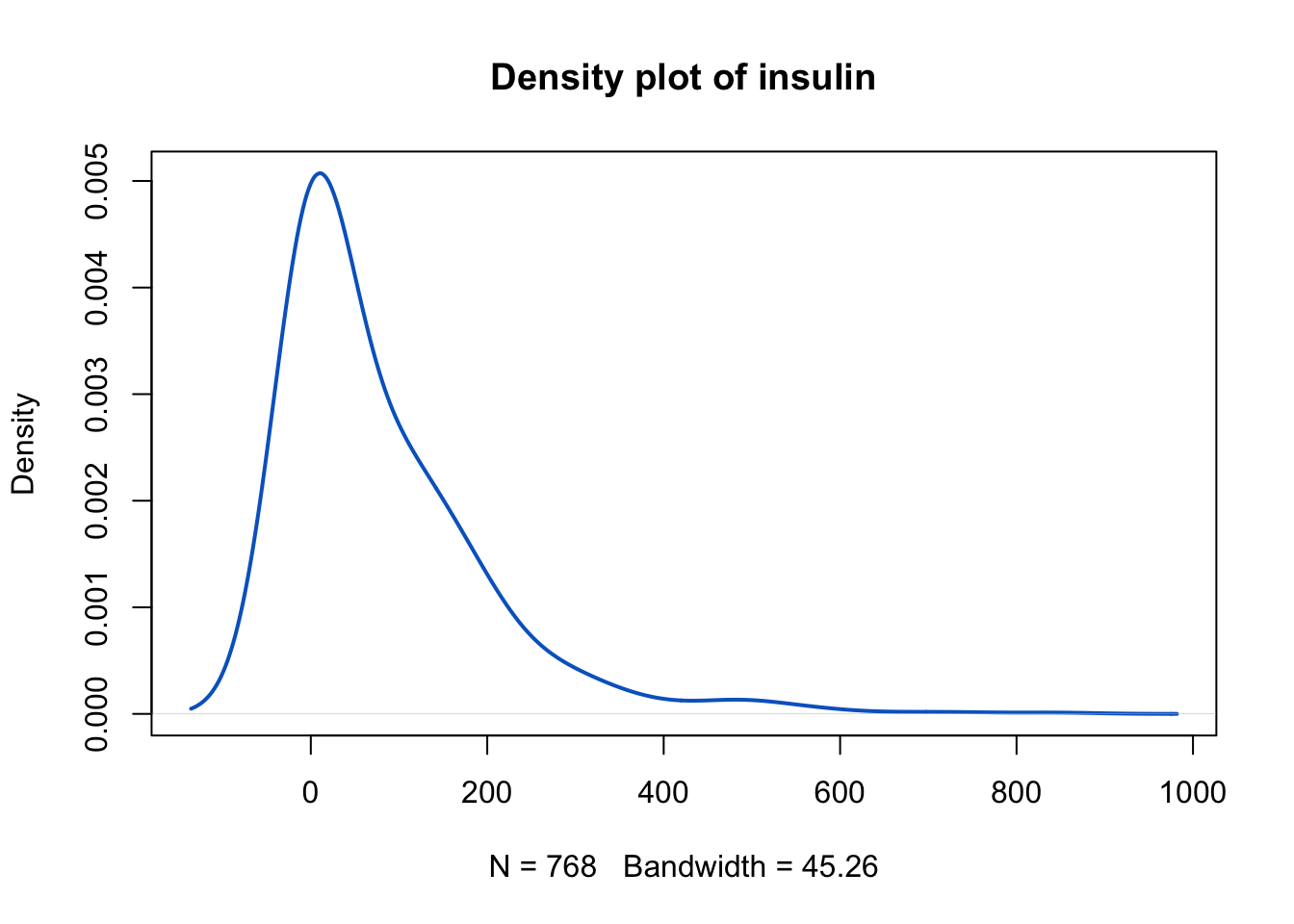
    )

      Click to show/hide code 
          # calculate skewness and its standard error
    library(psych)
    library(sasLM)
    paste(
"Skewness =", 
round(skew(PimaIndiansDiabetes$insulin, type = 2), 3)
    )
      [1] "Skewness = 2.272"
      Click to show/hide code 
          paste(
"Skewness SE =", 
round(SkewnessSE(PimaIndiansDiabetes$insulin), 3)
    )
      [1] "Skewness SE = 0.088"

  • These results are similar to the results obtained by SPSS or Graphpad Prism:

    SPSS

    Graphpad Prism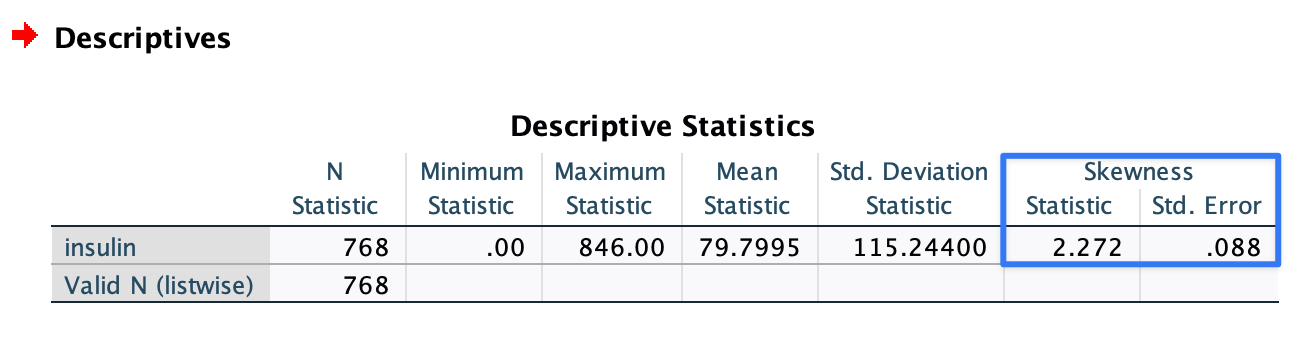

3 Kurtosis

  • It is a measure of tail heaviness (tailedness) of a distribution.

  • It is described as the standardized fourth moment \((m_4)\) of the distribution about the mean.

Kurtosis is not a measure of peakedness!
  • There is a misconception that kurtosis measures the peakedness, but actually its interpretation is in terms of tail extremity (Westfall 2014).

3.1 Formula

  • There are three formulas to calculate excess kurtosis (we will use sample moments):

    1. Raw formula \(g_2\):

      \[ g_2 = \displaystyle \frac{m_4}{m_2^2} - 3 \]

      • \(m_4\) is the fourth moment about the mean:

        \[ m_4 = \displaystyle \frac{1}{n} \sum_{i=1}^{n} (x_i - \bar{x})^4 \]

      • \(m_2\) is the second moment about the mean:

        \[ m_2 = \displaystyle \frac{1}{n} \sum_{i=1}^{n} (x_i - \bar{x})^2 \]

    2. Fisher’s \(G_2\):

      \[ G_2 = \displaystyle \frac{(n + 1)g_2 + 6}{(n - 2)(n - 3)} \]

      • This formula is used by SAS, SPSS, NCSS, Excel (KURT function), and Graphpad Prism.

    3. Kurtosis \(b_2\):

      \[ b_1 = \displaystyle \frac{m_4}{s^4} -3 = (g_2 +3)(1 - \displaystyle \frac{1}{n})^2 - 3 \]

      • \(s\) is the sample standard deviation \(\big [s = \sqrt{\displaystyle \frac{1}{n-1} \sum_{i=1}^{n} (x_i - \bar{x})^2} \big ]\).

      • This formula is used by Minitab.

  • The standard error of kurtosis is given by:

    \[ SE_{kurtosis} = \sqrt \frac{24n(n-1)^2}{(n-3)(n-2)(n+3)(n+5)} \]

3.2 Interpretation

  • Normal distribution is usually used as a reference, which has a kurtosis of \(3\) and is referred to as mesokurtic.

  • Unimodal distributions with kurtosis \(\gt 3\) possess heavier or thicker tails (i.e., more extreme values in the tails) relative to the normal distribution and are referred to as leptokurtic.

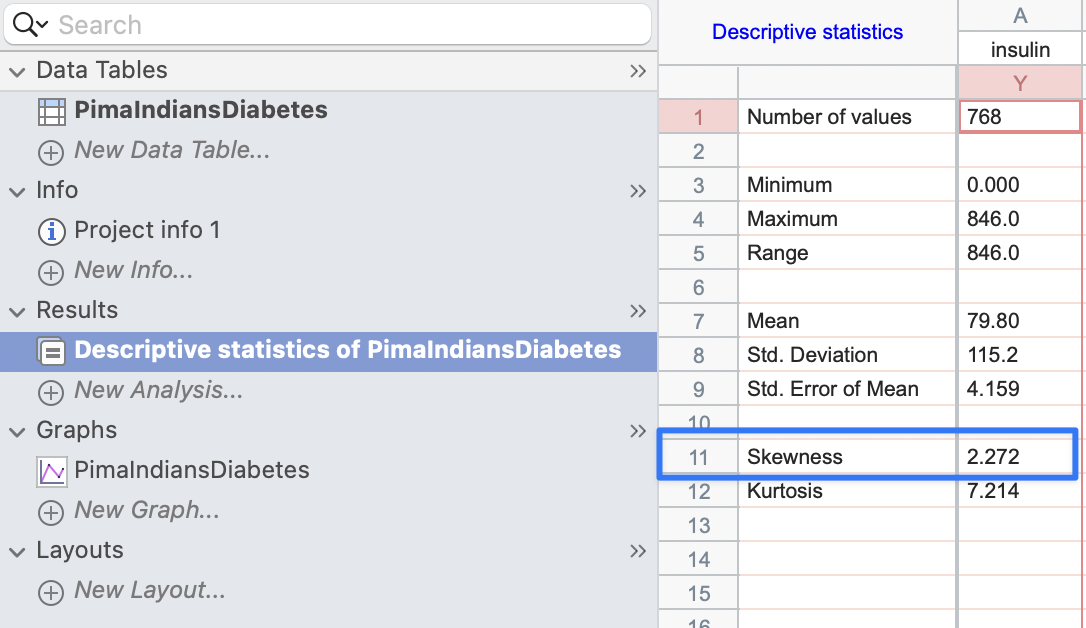
  • Unimodal distributions with kurtosis \(\lt 3\) possess lighter or thinner tails relative to the normal distribution and are referred to as platykurtic.

  • The following figure shows different distributions and their kurtosis values:

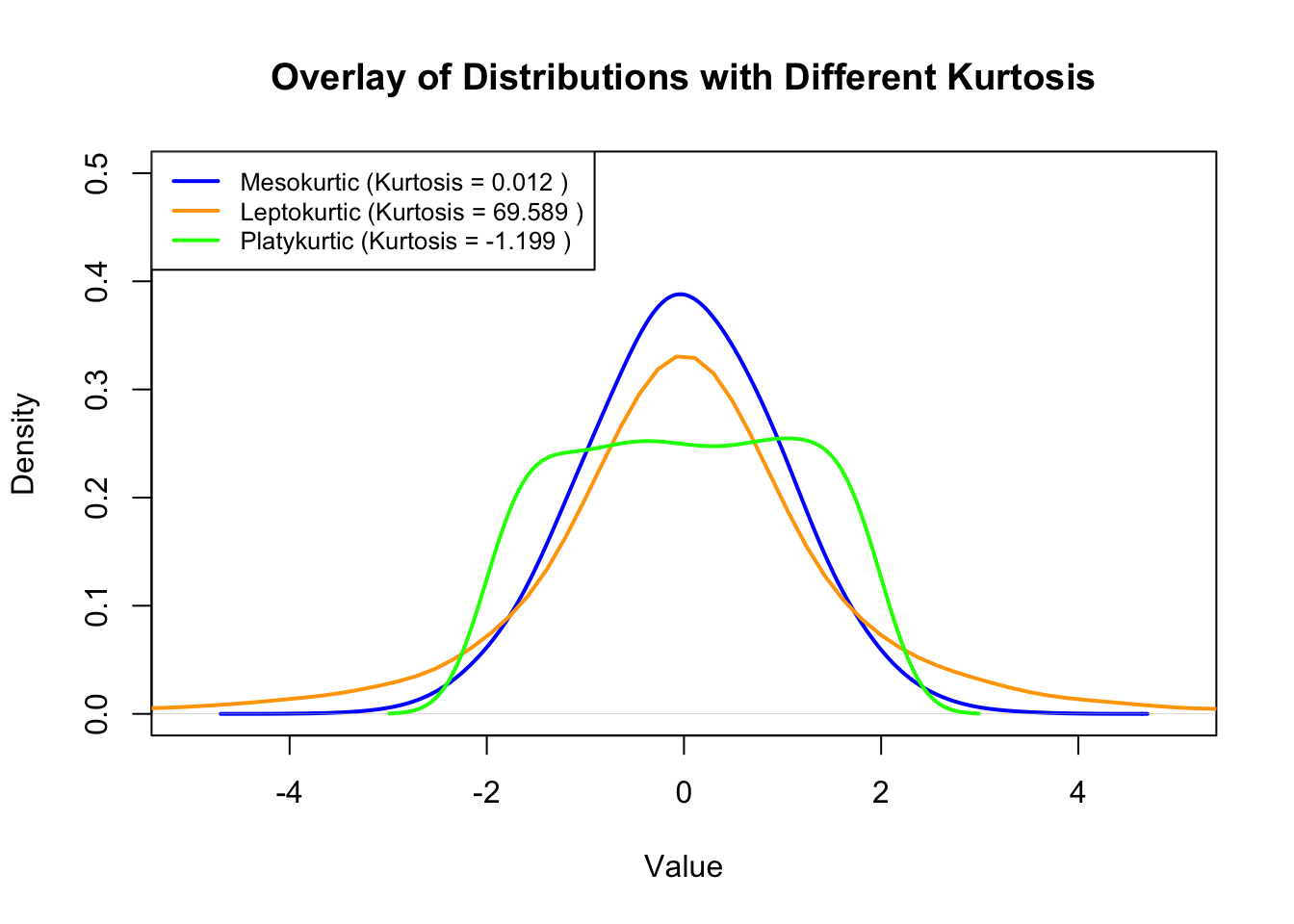
  • As depicted in the above figure, the mesokuotic distribution is a normal distribution that has a kurtosis of \(0\) because software packages express it as excess kurtosis \((Kurtosis - 3)\).

  • In this context, the leptokurtic distribution has a kurtosis \(\gt 0\), while the platykurtic distribution has a kurtosis \(\lt 0\).

3.3 Calculation in R

  • Different functions in R can be used to calculate the kurtosis:

    • kurtosis() function from the moments package (uses formula 1 but as raw kurtosis, i.e., \(m_4/m_2^2\)).

    • Kurtosis() function from the sasLM package (uses formula 2).

    • kurtosi() function from the psych package or kurtosis() function from the e1071 package can calculate skewness using the three formulas by setting the type argument to either \(1\), \(2\), or \(3\).

  • The skewness standard error can be calculated using the KurtosisSE() function from the sasLM package.

  • For example, the skewness of the insulin variable from the PimaIndiansDiabetes dataset can be calculated as follows:

    Click to show/hide code 
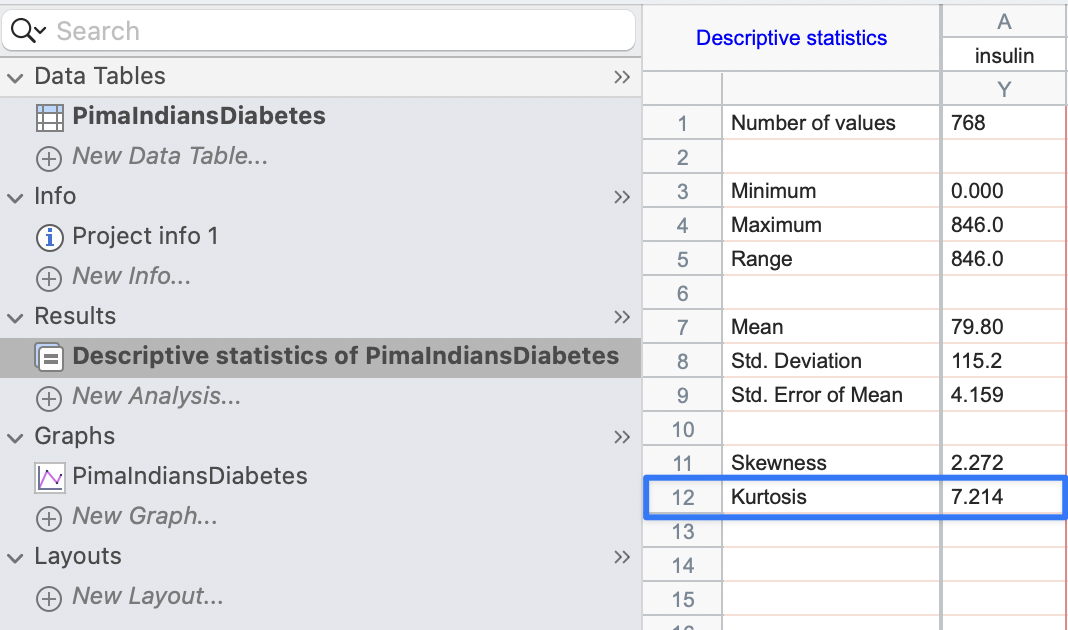
            # load the library and dataset
        library(mlbench)
        data(PimaIndiansDiabetes)

        # calculate kurtosis and its standard error
        library(psych)
        library(sasLM)
        paste(
    "Kurtosis =", 
    round(kurtosi(PimaIndiansDiabetes$insulin, type = 2), 3)
        )
    [1] "Kurtosis = 7.214"
    Click to show/hide code 
            paste(
    "Kurtosis SE =", 
    round(KurtosisSE(PimaIndiansDiabetes$insulin), 3)
        )
    [1] "Kurtosis SE = 0.176"

  • These results are similar to the results obtained by SPSS or Graphpad Prism:

    SPSS

    Graphpad Prism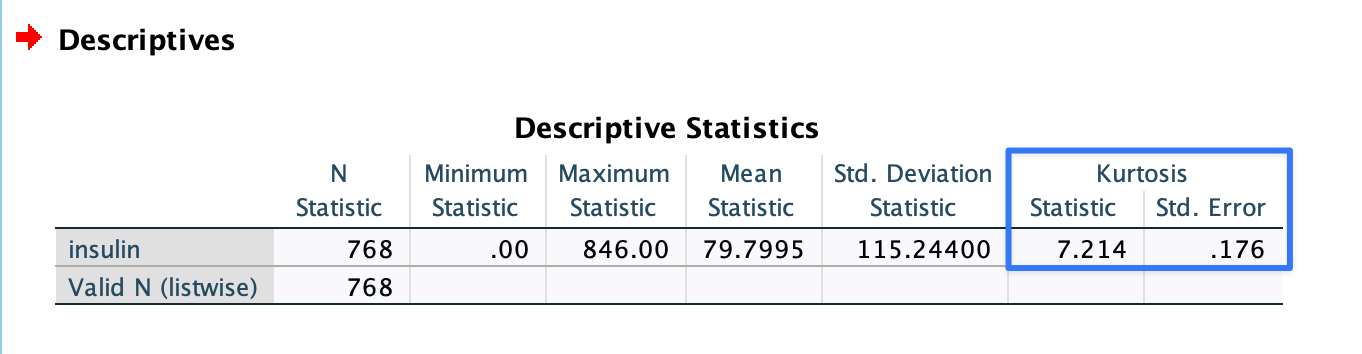

4 References

  • Daniel, W. W. and Cross, C. L. (2013). Biostatistics: A Foundation for Analysis in the Health Sciences, Tenth edition. Wiley

  • Heumann, C., Schomaker, M., and Shalabh (2022). Introduction to Statistics and Data Analysis: With Exercises, Solutions and Applications in R. Springer

  • Hoffman, J. (2019). Basic Biostatistics for Medical and Biomedical Practitioners, Second Edition. Academic Press

  • Lane, D. M. et al., (2019). Introduction to Statistics. Online Edition. Retrieved September 14, 2024, from https://openstax.org/details/introduction-statistics

  • Westfall, Peter H. 2014. Kurtosis as Peakedness, 1905–2014. R.I.P. The American Statistician 68 (3): 191–95. https://doi.org/10.1080/00031305.2014.917055


5 Add your comments

Back to top